题目内容
13.如图1,直线l交x轴、y轴分别于A、B两点,A(a,0),B(0,b),且(a-b)2+|b-4|=0.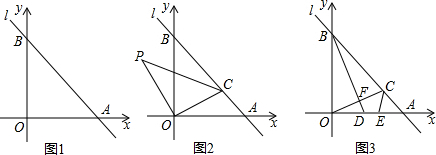
(1)求A、B两点坐标;
(2)如图2,C为线段AB上一点,且C点的横坐标是3.求△AOC的面积;
(3)如图2,在(2)的条件下,以OC为直角边作等腰直角△POC,请求出P点坐标;
(4)如图3,在(2)的条件下,过B点作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
分析 (1)先根据非负数的性质求出a、b的值,进而可得出AB两点的坐标;
(2)过C作CD⊥x轴于D,根据C点横坐标可得出OD的长,再由OA=OB可得出∠BAO=45°,故可得出CD的长,由三角形的面积公式即可得出结论;
(3)过P作PE⊥x轴于E,根据等腰直角三角形POC,证得∠EPO=∠COD,由AAS证得△EPO≌△DOC,得出OE=CD=1,PE=OD=3,即可求得P的坐标;
(4)过A作AG⊥x轴于A,交OC延长线于G.先证△BOD≌△OAG,证得∠BDO=∠G,OD=AG.由∠CEA=∠BDO,得出∠CEA=∠G.根据∠BAO=45°,∠GAO=90°,得出∠BAO=∠CAG=45°.然后根据AAS证得△CEA≌△CGA,得出AE=AG,即可证得OD=AE.
解答 解:(1)∵(a-b)2+|b-4|=0,
∴$\left\{\begin{array}{l}a-b=0\\ b-4=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=4\\ b=4\end{array}\right.$
∴A(4,0),B(0,4);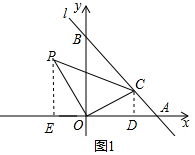
(2)如图1,过C作CD⊥x轴于D.
∵xC=3,A(4,0),B(0,4)
∴OD=3,OA=OB=4,
∴AD=OA-OD=1,∠BAO=45°,
∴CD=AD=1
∴S△AOC=$\frac{1}{2}$OA•CD=2,即△AOC的面积为2;
(3)如图1,过P作PE⊥x轴于E,
则∠PEO=∠CDO=90°,
∴∠EPO+∠EOP=90°.
∵△POC是等腰直角三角形,
∴OP=OC,∠POC=90°.
∴∠EOP+∠COD=90°.
∴∠EPO=∠COD.
在△EPO和△DOC中,
$\left\{\begin{array}{l}∠PEO=∠CDO\\∠EPO=∠COD\\ OP=OC\end{array}\right.$,
∴△EPO≌△DOC(AAS)
∴OE=CD=1,PE=OD=3,
∴P(-1,3);
(4)OD=AE.理由如下:
如图2,过A作AG⊥x轴于A,交OC延长线于G.
∴∠GAO=90°.
∵OB⊥OA,BD⊥OC,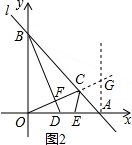
∴∠BOD=∠BFO=90°,
∴∠OBD+∠BOF=∠AOF+∠BOF=90°.
∴∠OBD=∠AOF.
在△BOD和△OAG中,
$\left\{\begin{array}{l}∠BOD=∠GAO=90°\\ OB=OA\\∠OBD=∠AOG\end{array}\right.$,
∴△BOD≌△OAG(ASA)
∴∠BDO=∠G,OD=AG.
∵∠CEA=∠BDO,
∴∠CEA=∠G.
∵∠BAO=45°,∠GAO=90°,
∴∠BAO=∠CAG=45°.
在△CEA和△CGA中,
$\left\{\begin{array}{l}∠CEA=∠D\\∠CAE=∠CAG\\ AC=AC\end{array}\right.$,
∴△CEA≌△CGA(AAS),
∴AE=AG,
∴OD=AE.
点评 本题考查了等腰直角三角形的判定和性质,三角形全等的判定和性质,作出辅助线构建直角三角形是解题的关键.

| A. | 前十名学生的印象 | B. | 后十名学生的印象 | ||
| C. | 全体男学生的印象 | D. | 单号学号学生的印象 |
| A. | $\frac{S^2}{2}$ | B. | S2 | C. | 4S2 | D. | 16S2 |
 如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC,且交AC于点E.
如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC,且交AC于点E. 如图,在△ABC中,DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求BF的长.
如图,在△ABC中,DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求BF的长.