题目内容
4.下列二次根式属于最简二次根式的是( )| A. | $\sqrt{12}$ | B. | $\sqrt{{a}^{2}b}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{x{\;}^{2}+1}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查定义中的两个条件(①被开方数不含分母;②被开方数不含能开得尽方的因数或因式)是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{12}$=$\sqrt{4×3}$=2$\sqrt{3}$被开方数里含有能开得尽方的因数4;故本选项错误;
B、$\sqrt{{a}^{2}b}$=$a\sqrt{b}$,被开方数里含有能开得尽方的因式a2;故本选项错误;
C、$\sqrt{0.5}=\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$被开方数里含有分母;故本选项错误;
$\sqrt{12}$=$\sqrt{4×3}$=2$\sqrt{3}$被开方数里含有能开得尽方的因数4;故本选项错误;
D、$\sqrt{{x}^{2}+1}$符合最简二次根式的条件;故本选项正确.
故选D.
点评 本题主要考查了最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
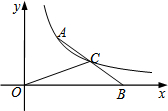 如图,A为双曲线y=$\frac{4}{x}$(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OBC的面积为( )
如图,A为双曲线y=$\frac{4}{x}$(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OBC的面积为( )