题目内容
19.解二元一次方程组:(1)$\left\{\begin{array}{l}y=3x-2\\ 6x-3y=5\end{array}\right.$(代入法)
(2)$\left\{\begin{array}{l}\frac{x}{2}+\frac{y}{3}=2\\ 2x+3y=28\end{array}\right.$(加减法)
分析 (1)根据代入消元法,可得方程组的解;
(2)根据加减消元法,可得方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{y=3x-2①}\\{6x-3y=5②}\end{array}\right.$,
把①代入②得
6x-3(3x-2)=5,解得x=$\frac{1}{3}$,
把x=$\frac{1}{3}$代入①得y=-1,
原方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-1}\end{array}\right.$,
(2)化简方程组,得
$\left\{\begin{array}{l}{6x+4y=24①}\\{6x+9y=84②}\end{array}\right.$,
②-①,得
5y=60,解得y=12,
把y=12代入①得x=-4
原方程组的解为$\left\{\begin{array}{l}{x=-4}\\{y=12}\end{array}\right.$.
点评 本题考查二元一次方程组和三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解二元一次方程组较简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.某红外线波长为0.00 000 094m,用科学记数法把0.00 000 094m可以写成( )
| A. | 9.4×10-7m | B. | 9.4×107m | C. | 9.4×10-8m | D. | 9.4×108m |
7.把二次函数y=-(x-2)2+6的图象向右平移2个单位,再向上平移3个单位,所得到图象的函数解析式是( )
| A. | y=-(x-4)2+9 | B. | y=-x2+9 | C. | y=-(x-5)2+8 | D. | y=-x2+8 |
14.如果x-$\frac{1}{x}$=3,则${x^2}+\frac{1}{x^2}$的值为( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
4.下列二次根式属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{a}^{2}b}$ | C. | $\sqrt{0.5}$ | D. | $\sqrt{x{\;}^{2}+1}$ |
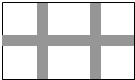 学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.
学校课外生物小组的试验园地是长20米宽15米的长方形.为了便于管理,现要在中间开辟一横两纵等宽的小道(如图),要使种植面积为252平方米,求小道的宽.