题目内容
 小明从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=
小明从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=| 5 |
| 13 |
(1)小明从A点到点B上升的高度是多少米?
(2)小明从A点到点C上升的高度CD是多少米?(结果保留根号)
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)根据题意画出图形,进而利用锐角三角函数关系分别求出BF;
(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.
(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.
解答: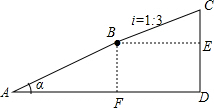 解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
由题意得:AB=650米,BC=1千米,
∴sinα=
=
=
,
∴BF=650×
=250米,
∴小明从A点到点B上升的高度是250米;
(2)∵斜坡BC的坡度为:1:3,
∴CE:BE=1:3,
设CE=x,则BE=3x,
由勾股定理得:x2+(3x)2=5002
解得:x=50
,
∴CD=CE+DE=BF+CE=250+50
,
答:点C相对于起点A升高了(250+50
)米.
 解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,由题意得:AB=650米,BC=1千米,
∴sinα=
| 5 |
| 13 |
| BF |
| AB |
| BF |
| 650 |
∴BF=650×
| 3 |
| 13 |
∴小明从A点到点B上升的高度是250米;
(2)∵斜坡BC的坡度为:1:3,
∴CE:BE=1:3,
设CE=x,则BE=3x,
由勾股定理得:x2+(3x)2=5002
解得:x=50
| 10 |
∴CD=CE+DE=BF+CE=250+50
| 10 |
答:点C相对于起点A升高了(250+50
| 10 |
点评:此题主要考查了解直角三角形的应用,正确选择锐角三角函数得出BF,CE的长是解题关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
若3x-1和4x+8的值相等,则x的值为( )
| A、-7 | ||
| B、-9 | ||
C、-
| ||
| D、-1 |
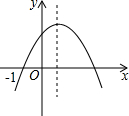 已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列四个结论:①a<0;②a+b+c>0;③-
已知抛物线y=ax2+bx+c(a≠0)经过点(-1,0),且顶点在第一象限.有下列四个结论:①a<0;②a+b+c>0;③-


