题目内容
函数y=ax2+c和y=
(a≠0,c≠0)在同一坐标系里的图象大致是( )
| a |
| x |
A、 |
B、 |
C、 |
D、 |
考点:二次函数的图象,反比例函数的图象
专题:
分析:本题可先由二次函数图象得到字母系数的正负,再与反比例函数的图象相比较看是否一致.逐一排除.
解答:解:由A,D中的二次函数图象可得a>0,c=0,因为y=
(a≠0,c≠0),故A,D错误;
由B,C中的二次函数图象可得a<0,c>0,所以y=
(a≠0,c≠0)的图象在二,四象限内,故C错误,B正确.
故选:B.
| a |
| x |
由B,C中的二次函数图象可得a<0,c>0,所以y=
| a |
| x |
故选:B.
点评:此题主要考查了反比例函数图象与二次函数图象,应该识记反比例函数在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴等.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
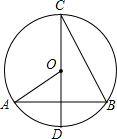 如图,在⊙O中,直径CD垂直弦AB,连接OA,CB,已知⊙O的半径为2,AB=2
如图,在⊙O中,直径CD垂直弦AB,连接OA,CB,已知⊙O的半径为2,AB=2| 3 |
| A、20° | B、30° |
| C、60° | D、70° |
将Rt△ABC的三边分别扩大2倍,得到Rt△A′B′C′,则( )
| A、sinA=sinA′ |
| B、sinA>sinA′ |
| C、sinA<sinA′ |
| D、不能确定 |
下列运算中正确的是( )
| A、a4•a2=a8 |
| B、(3a)2=6a2 |
| C、6a-2a=4a |
| D、a5-a2=a3 |
点A(m2+1,yA)在正比例函数y=-2x的图象上,则( )
| A、yA>0 |
| B、yA<0 |
| C、yA≤-2 |
| D、yA≥-2 |
下列计算正确的是( )
| A、x4•x4=x16 |
| B、(a5)2=a7 |
| C、(ab2)3=ab6 |
| D、(-y)10÷(-y)7=-y3 |
不等式4x-7≥5(x-1)的解集是( )
| A、x≥2 | B、x≥-2 |
| C、x≤-2 | D、x≤2 |
 小明从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=
小明从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=