题目内容
两相似三角形面积之比为1:4,则它们的周长之比为 ( )
| A、1:4 | B、1:16 |
| C、1:2 | D、1:8 |
考点:相似三角形的性质
专题:
分析:由两相似三角形面积之比为1:4,根据相似三角形的面积比等于相似比的平方,即可求得其相似比,又由相似三角形的周长的比等于相似比,即可求得答案.
解答:解:∵两相似三角形面积之比为1:4,
∴它们的相似比为1:2,
∴它们的周长之比为1:2.
故选C.
∴它们的相似比为1:2,
∴它们的周长之比为1:2.
故选C.
点评:此题考查了相似三角形的性质.此题比较简单,注意熟记定理是解此题的关键.

练习册系列答案
相关题目
一个多边形有五条对角线,则这个多边形的边数为( )
| A、8 | B、7 | C、6 | D、5 |
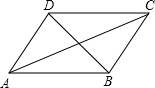 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
如图,四边形ABCD是平行四边形,下列说法不正确的是( )| A、当AC=BD时,四边形ABCD是矩形 |
| B、当∠DAB=90°时,四边形ABCD是正方形 |
| C、当AC⊥BD时,四边形ABCD是菱形 |
| D、当AB=BC时,四边形ABCD是菱形 |
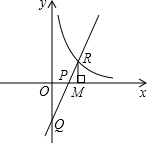 如图,直线y=kx-1(k>0)与双曲线y=
如图,直线y=kx-1(k>0)与双曲线y=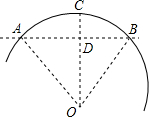 建造一座跨度为36米的圆弧拱桥,要求拱桥的顶端离地平线的高度为7米,试计算拱桥桥面的长度.已知:如图,
建造一座跨度为36米的圆弧拱桥,要求拱桥的顶端离地平线的高度为7米,试计算拱桥桥面的长度.已知:如图,
 如图,∵∠1=74°(已知)
如图,∵∠1=74°(已知)