题目内容
3.求出该方程中x的值:(1)32(x-1)3=$\frac{27}{2}$
(2)3(5x+1)2-48=0.
分析 (1)根据解方程的方法和立方根的定义可以解答本题;
(2)根据解方程的方法和平方根的定义可以解答本题
解答 解:(1)32(x-1)3=$\frac{27}{2}$
$(x-1)^{3}=\frac{27}{64}$
x-1=$\frac{3}{4}$,
x=$\frac{7}{4}$;
(2)3(5x+1)2-48=0
3(5x+1)2=48
(5x+1)2=16
5x+1=±4
解得,${x}_{1}=\frac{3}{5},{x}_{2}=-1$.
点评 本题考查平方根、立方根、解方程,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
13.下列方程中,属于二元一次方程的是( )
| A. | 4x+2(8-5x)=3 | B. | $\frac{1}{5}$x-3y=6 | C. | x2+4y=9 | D. | xy+2x=5 |
8.在下列图案中,既是中心对称,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 在Rt△ABC中,∠BAC=90°,D是BC中点,E是AD中点,过A作AF∥BC
在Rt△ABC中,∠BAC=90°,D是BC中点,E是AD中点,过A作AF∥BC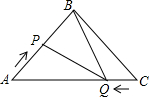 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.