题目内容
17.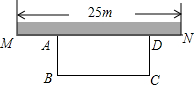 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可供利用25m),现在已备足可以砌50m长的墙的材料.(1)试设计一种砌法,使矩形花园的面积为300m2;
(2)是否存在使矩形花园面积最大的砌法?如果存在,说明砌法;如果不存在,请说明理由.
分析 (1)根据可以砌50m长的墙的材料,即总长度是50米,AB=x米,则BC=(50-2x)米,再根据矩形的面积公式列方程,解一元二次方程即可;
(2)设边AB的长是x米,则BC=(40-2x)米.利用矩形的面积公式列出函数关系是即可,然后利用配方法求得函数的最大值即可;
解答 解:(1)设AB=x米,则BC=(50-2x)米.
根据题意可得,x(50-2x)=300,
解得:x1=10,x2=15,
当x=10,BC=50-10-10=30>25,
故x1=10(不合题意舍去),
当x=15时,BC=50-2×15=20(米).
答:可以围成AB的长为15米,BC为20米的矩形;解:(1)设边AB的长是x米,则BC=(37+3-2x)=(40-2x)米.
(2)存在,根据题意得:y=x(50-2x)=-2(x-$\frac{25}{2}$)+3125,
∴当AB=$\frac{25}{2}$m,BC=25m时,矩形花园面积最大.
点评 本题主要考查的是二次函数的应用,一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系求解,注意围墙MN最长可利用25m,舍掉不符合题意的数据,根据题意列出关于函数的解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 探究气球的气象观测统计资料表明,高度每增加1km,气温降低大约6℃,现在地面气温是21℃,如果气球竖起上升的平均速度为1m/s,那么气球经过5小时飞行后所在高空处的气温约是多少摄氏度?
探究气球的气象观测统计资料表明,高度每增加1km,气温降低大约6℃,现在地面气温是21℃,如果气球竖起上升的平均速度为1m/s,那么气球经过5小时飞行后所在高空处的气温约是多少摄氏度? 已知:如图,∠ACE=∠BCD,AE=BD,∠A=∠B.求证:C是AB的中点.
已知:如图,∠ACE=∠BCD,AE=BD,∠A=∠B.求证:C是AB的中点.