题目内容
18.解下列方程(1)(2x-1)2=9.
(2)7x(5x+2)=6(5x+2)
(3)x2-2x-35=0.
(4)3x2+2(x-1)=0.
(5)$\left\{\begin{array}{l}2x-y=3\\ 3x+2y=7\end{array}\right.$.
分析 (1)方程利用平方根定义开方即可求出解;
(2)方程移项后,利用因式分解法求出解即可;
(3)方程利用因式分解法求出解即可;
(4)方程整理后,利用公式法求出解即可;
(5)方程组利用加减消元法求出解即可.
解答 解:(1)开方得:2x-1=3或2x-1=-3,
解得:x1=2,x2=-1;
(2)方程移项得:7x(5x+2)-6(5x+2)=0,
分解因式得:(7x-6)(5x+2)=0,
解得:x1=$\frac{6}{7}$,x2=-$\frac{2}{5}$;
(3)分解因式得:(x-7)(x+5)=0,
解得:x1=7,x2=-5;
(4)方程整理得:3x2+2x-2=0,
这里a=3,b=2,c=-2,
∵△=4+24=28,
∴x=$\frac{-2±2\sqrt{7}}{6}$=$\frac{-1±\sqrt{7}}{3}$;
(5)$\left\{\begin{array}{l}{2x-y=3①}\\{3x+2y=7②}\end{array}\right.$,
①×2+②得:7x=13,即x=$\frac{13}{7}$,
把x=$\frac{13}{7}$代入①得:y=$\frac{5}{7}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{13}{7}}\\{y=\frac{5}{7}}\end{array}\right.$.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
6.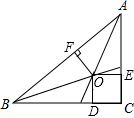 如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
 如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )| A. | 2cm、2cm、2cm | B. | 3cm、3cm、3cm | C. | 4cm、4cm、4cm | D. | 2cm、3cm、5cm |
13. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
8.在二次函数y=x2+bx+c中,函数值y与自变量x的部分对应值如表,则该抛物线的顶点坐标为(1,-2),m=-1.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 7 | 2 | -1 | -2 | m | 2 | 7 |
 如图,△ABC经过一定的变换得到△A1B1C1,若△ABC上一点M的坐标为(m,n),那么M的对应点M1的坐标为(m+4,n+2).
如图,△ABC经过一定的变换得到△A1B1C1,若△ABC上一点M的坐标为(m,n),那么M的对应点M1的坐标为(m+4,n+2). 在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.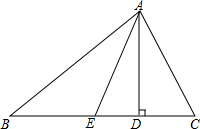 如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论:
如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论: