题目内容
11. 如图所示,在△ABC中,AD⊥BC,D为垂足,AE是△ABC中∠BAC的平分线,∠B=45°,∠AED=80°,求∠C,∠EAD的度数.
如图所示,在△ABC中,AD⊥BC,D为垂足,AE是△ABC中∠BAC的平分线,∠B=45°,∠AED=80°,求∠C,∠EAD的度数.
分析 先根据三角形外角的性质计算出∠BAE=35°,再根据角平分线定义得到∠BAC=2∠BAE=70°,则在△ABC中根据三角形内角和定理可计算出∠C=180°-∠B-∠BAC=75°,接着根据垂直的定义得到∠ADE=90°,然后利用∠EAD=90°-∠AED进行计算即可.
解答 解:∵∠B=45°,∠AED=80°,
∴∠BAE=∠AED-∠B=35°,
∵AE是△ABC中∠BAC的平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=65°,
∵AD⊥BC,D为垂足,
∴∠ADE=90°,
∴∠EAD=90°-∠AED=10°.
点评 本题考查了三角形的角平分线、中线和高,三角形内角和定理及外角的性质.准确识别图形是解题的关键.

练习册系列答案
相关题目
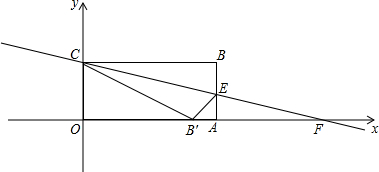
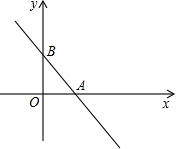 已知:一次函数y=-$\frac{4}{3}$x+4的函数与x轴、y轴交于A、B两点.
已知:一次函数y=-$\frac{4}{3}$x+4的函数与x轴、y轴交于A、B两点. 已知:如图,△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F,求证:四边形CDEF是菱形.
已知:如图,△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F,求证:四边形CDEF是菱形.