题目内容
18.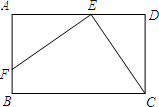 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.
分析 先证∠AEF=∠ECD,再证Rt△AEF≌Rt△DCE,然后结合题目中已知的线段关系求解.
解答 解:在Rt△AEF和Rt△DEC中,EF⊥CE.
∴∠FEC=90°.
∴∠AEF+∠DEC=90°.
而∠ECD+∠DEC=90°.
∴∠AEF=∠ECD,
在△AEF与△DCE中,
$\left\{\begin{array}{l}{∠FAE=∠EDC=90°}\\{∠AEF=∠ECD}\\{EF=EC}\end{array}\right.$,
∴△AEF≌△DCE(AAS).
∴AE=CD,
AD=AE+4.
∵矩形ABCD的周长为32cm.
∴2(AE+ED+DC)=32,即2(2AE+4)=32,
整理得:2AE+4=16
解得:AE=6(cm).
故答案为6.
点评 本题综合考查了矩形的性质,三角形全等的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9.4的平方根是( )
| A. | ±2 | B. | 16 | C. | -2 | D. | 2 |
13.在$\sqrt{2}$,-3,4,$\frac{1}{2}$四个数中,无理数是( )
| A. | $\sqrt{2}$ | B. | -3 | C. | 4 | D. | $\frac{1}{2}$ |
3.观察下列各数:1,$\frac{4}{3}$,$\frac{9}{7}$,$\frac{16}{15}$,…,按你发现的规律计算这列数的第6个数为( )
| A. | $\frac{25}{31}$ | B. | $\frac{36}{35}$ | C. | $\frac{4}{7}$ | D. | $\frac{62}{63}$ |
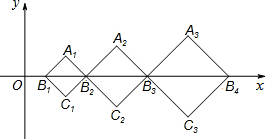 如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.
如图所示,在平面直角坐标系xOy中,B1(1,0),B2(3,0),B3(6,0),B4(10,0),…,以B1B2为对角线作第一个正方形A1B1C1B2,以B2B3为对角线作第二个正方形A2B2C2B3,以B3B4为对角线作第三个正方形A3B3C3B4,…,如果所作正方形的对角线BnBn+1的长度依次增加1个单位长度,顶点An都在第一象限内(n≥1,且n为整数),用n的代数式表示An的横坐标为$\frac{(π+1)^{2}}{2}$.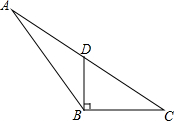 如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.