题目内容
12.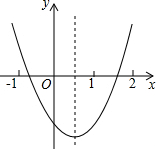 如图,观察二次函数y=ax2+bx+c的图象,下列结论:
如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,③b2-4ac>0,④ac>0.
其中正确的是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
分析 令x=1代入可判断①;由对称轴x=-$\frac{b}{2a}$的范围可判断②;由图象与x轴有两个交点可判断③;由开口方向及与x轴的交点可分别得出a、c的符号,可判断④.
解答 解:由图象可知当x=1时,y<0,
∴a+b+c<0,
故①不正确;
由图象可知0<-$\frac{b}{2a}$<1,
∴$\frac{b}{2a}$>-1,
又∵开口向上,
∴a>0,
∴b>-2a,
∴2a+b>0,
故②正确;
由图象可知二次函数与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△>0,即b2-4ac>0,
故③正确;
由图象可知抛物线开口向上,与y轴的交点在x轴的下方,
∴a>0,c<0,
∴ac<0,
故④不正确;
综上可知正确的为②③,
故选C.
点评 本题主要考查二次函数的图象和性质,掌握二次函数的开口方向、对称轴、与x轴的交点等知识是解题的关键.

练习册系列答案
相关题目
2.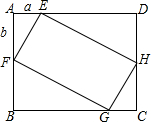 如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
 如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )| A. | $\left\{\begin{array}{l}{a+b=4}\\{a+2b=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2a+b=4}\\{a+2b=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2b}\\{2a+b=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=4}\end{array}\right.$ |
3.观察下列各数:1,$\frac{4}{3}$,$\frac{9}{7}$,$\frac{16}{15}$,…,按你发现的规律计算这列数的第6个数为( )
| A. | $\frac{25}{31}$ | B. | $\frac{36}{35}$ | C. | $\frac{4}{7}$ | D. | $\frac{62}{63}$ |
1.一个正常人的心跳平均每分70次,一天大约跳100800次,将100800用科学记数法表示为( )
| A. | 0.1008×106 | B. | 1.008×106 | C. | 1.008×105 | D. | 10.08×104 |




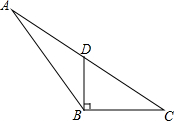 如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.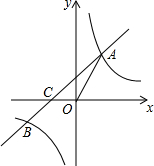 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.