题目内容
18.化简:$\frac{2}{b}$$\sqrt{a{b}^{3}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)÷3$\sqrt{\frac{b}{a}}$(a>0,b>0)分析 根据二次根式乘除法的性质将原式转化为-$\frac{2}{b}$$\sqrt{a{b}^{3}}$•$\frac{3}{2}$$\sqrt{{a}^{3}b}$•$\frac{1}{3}$$\sqrt{\frac{a}{b}}$,化简即可.
解答 解:原式=-$\frac{2}{b}$$\sqrt{a{b}^{3}}$•$\frac{3}{2}$$\sqrt{{a}^{3}b}$•$\frac{1}{3}$$\sqrt{\frac{a}{b}}$
=-$\frac{1}{b}$$\sqrt{{ab}^{3}•{a}^{3}b•\frac{a}{b}}$
=-$\frac{1}{b}$a2b$\sqrt{ab}$
=-a2$\sqrt{ab}$.
点评 本题考查了二次根式的乘除法,熟悉二次根式的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知二次函数y=a(x-m)2+k(a<0)经过点(0,5),(10,8),则m的值可以是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 11 |
6. 已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:
已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:
①当△ABC为等边三角形时,△ODE是等边三角形;
②当△ODE是等边三角形,△ABC为等边三角形;
③当∠A=45°时,△ODE是直角三角形;
④当△ODE是直角三角形时,∠A=45°.
正确的结论有( )
 已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:
已知,如图,以△ABC的一边BC为直径的⊙O分别交AB、AC于D、E,下面判断中:①当△ABC为等边三角形时,△ODE是等边三角形;
②当△ODE是等边三角形,△ABC为等边三角形;
③当∠A=45°时,△ODE是直角三角形;
④当△ODE是直角三角形时,∠A=45°.
正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列计算,正确的是( )
| A. | (x3)2=x5 | B. | x3•x2=x5 | C. | (2x)2=2x3 | D. | (x+1)2=x3+1 |
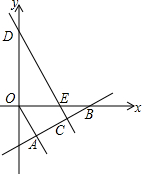 如图,直线y=$\frac{1}{2}$x-$\frac{11}{2}$与x轴交于B,与直线y=-$\frac{4}{3}$x相交于A,线段AB的垂直平分线CD分别与AB,x轴,y轴交于点C,E,D.
如图,直线y=$\frac{1}{2}$x-$\frac{11}{2}$与x轴交于B,与直线y=-$\frac{4}{3}$x相交于A,线段AB的垂直平分线CD分别与AB,x轴,y轴交于点C,E,D.