点M是AB的中点.∠1=∠2.∠C=∠D.试说明△CAM≌△DBM．题目和参考答案——青夏教育精英家教网—

题目内容

14．

点M是AB的中点，∠1=∠2，∠C=∠D，试说明△CAM≌△DBM．

分析根据两角和其中一角的对边对应相等的两个三角形全等即可判定．

解答证明：如图，∵点M是AB中点，
∴AM=BM，
在△CAM和△DBM中，
$\left\{\begin{array}{l}{∠C=∠D}\\{∠1=∠2}\\{AM=BM}\end{array}\right.$，
∴△CAM≌△DBM．

点评本题考查全等三角形的判定，解题的关键是熟练掌握全等三角形的判定方法，属于基础题，中考常考题型．

练习册系列答案

5．

如图是一几何体的三视图，这个几何体可能是（　　）

2．

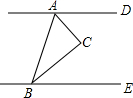若AD∥BE，AC平分∠DAB，CB平分∠ABE，∠CBE=30°，则∠CAD的度数为（　　）

9．关于x的一元二次方程mx²+4x+1=0有两个实数根，那么m的取值范围是m≤4且m≠0．

19．解下列不等式组，并在数轴上表示解集．
（1）$\left\{\begin{array}{l}{2x+3＞5}\\{3x-2≤4}\end{array}\right.$
（2）$\left\{\begin{array}{l}{-2x+1＞-11}\\{\frac{3x+1}{2}-1≥x}\end{array}\right.$．

6．关于x，y的二元一次方程组$\left\{\begin{array}{l}{x+y=2k}\\{2-4y=4k+1}\end{array}\right.$的解满足x＞y，求k的范围．

5．已知抛物线y=ax²-2ax+m与x轴相交于A（-1，0）、B两点，与y轴负半轴相交于点C，且S_△ABC=6，则（　　）

	A．	在y轴右侧该抛物线上不存在点M，使S_△ACM=3
	B．	在y轴右侧该抛物线上存在两个点M，使S_△ACM=3
	C．	在y轴右侧该抛物线上存在唯一的点M（2，3），使S_△ACM=3
	D．	在y轴右侧该抛物线上存在唯一的点M（2，-3），使S_△ACM=3

6．下列数值中，是不等式x≥-2的解的是（　　）

试题分类