题目内容
(1)已知:如图(1),点M在锐角∠AOB的内部,在边OA上求作一点P,在边OB上求作一点Q,使得△PMQ的周长最小;
(2)已知:如图(2),点M在锐角∠AOB的内部,在边OB上求作一点P,使得点P到点M的距离与点P到边OA的距离之和最小.
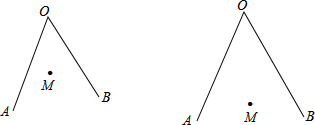
(2)已知:如图(2),点M在锐角∠AOB的内部,在边OB上求作一点P,使得点P到点M的距离与点P到边OA的距离之和最小.
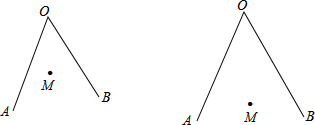
考点:轴对称-最短路线问题
专题:
分析:(1)根据轴对称确定最短路线问题,作出点M关于OA的对称点M1,点M关于OB的对称点M2,连接M1M2,与OA、OB的交点即为所求的点P、Q;
(2)作出点M关于OB的对称点M′,根据垂线段最短,作M′C⊥OA,与OB的交点即为所求作的点P.
(2)作出点M关于OB的对称点M′,根据垂线段最短,作M′C⊥OA,与OB的交点即为所求作的点P.
解答:解:(1)如图所示,点P、Q即为所求作的使△PMQ的周长最小的点;
(2)如图所示,点P到点M的距离与点P到边OA的距离之和最小.

(2)如图所示,点P到点M的距离与点P到边OA的距离之和最小.

点评:本题考查了轴对称确定最短路线问题,主要利用了对称点的作法和轴对称的性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
平面直角坐标系中,半径均为
的两圆的圆心坐标分别是(0,0)和(0,2),则两圆的位置关系是( )
| 2 |
| A、内含 | B、相交 | C、外切 | D、外离 |
下列图形是几种汽车的标志,其中是中心对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
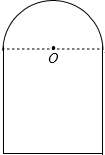 如图所示为上边是半圆,下边是长方形的桥洞,已知半圆的直径为2.2米,长方形的另一边为2.3米,有一辆装满货物的卡车,高2.5米,宽1.6米,要从此桥洞经过.
如图所示为上边是半圆,下边是长方形的桥洞,已知半圆的直径为2.2米,长方形的另一边为2.3米,有一辆装满货物的卡车,高2.5米,宽1.6米,要从此桥洞经过.