题目内容
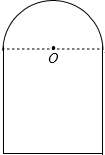 如图所示为上边是半圆,下边是长方形的桥洞,已知半圆的直径为2.2米,长方形的另一边为2.3米,有一辆装满货物的卡车,高2.5米,宽1.6米,要从此桥洞经过.
如图所示为上边是半圆,下边是长方形的桥洞,已知半圆的直径为2.2米,长方形的另一边为2.3米,有一辆装满货物的卡车,高2.5米,宽1.6米,要从此桥洞经过.(1)卡车是否能通过桥洞?说明理由.
(2)为了适应车流量的增加,先把桥洞改为双行道,要使宽为1.5米,高为3.1米的卡车通过,则桥洞的宽至少增加到多少米?
考点:垂径定理的应用,勾股定理
专题:
分析:(1)过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,根据卡车的宽和半圆的直径和勾股定理求出OE的长,再根据长方形的一边长和卡车的高即可得出答案;
(2)根据已知条件求出BF的长,再根据勾股定理求出OA的长,从而得出答案.
(2)根据已知条件求出BF的长,再根据勾股定理求出OA的长,从而得出答案.
解答: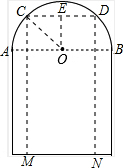 解:(1)如图,M,N为卡车的宽度,
解:(1)如图,M,N为卡车的宽度,
过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
CD=MN=1.6米,AB=2.2米,
由作法得,CE=DE=0.8米,
又∵OC=OA=1.1米,
在Rt△OCE中,OE=
=
=
≈0.75(米),
∴CM=2.3+0.75=3.05>2.5.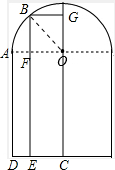
∴这辆卡车能通过.
(2)如图:
根据题意可知:CG=BE=3.1米,BG=OF=1.5米,EF=AD=2.3米,
∴BF=0.8米
∴根据勾股定理有:OA2=OB2=BF2+OF2=0.82+1.52=2.89(米),
∴OA=1.7米,
∴桥洞的宽至少增加到1.7×2=3.4(米).
 解:(1)如图,M,N为卡车的宽度,
解:(1)如图,M,N为卡车的宽度,过M,N作AB的垂线交半圆于C,D,过O作OE⊥CD,E为垂足,
CD=MN=1.6米,AB=2.2米,
由作法得,CE=DE=0.8米,
又∵OC=OA=1.1米,
在Rt△OCE中,OE=
| OC2-CE2 |
| 1.12-0.82 |
| ||
| 10 |
∴CM=2.3+0.75=3.05>2.5.

∴这辆卡车能通过.
(2)如图:
根据题意可知:CG=BE=3.1米,BG=OF=1.5米,EF=AD=2.3米,
∴BF=0.8米
∴根据勾股定理有:OA2=OB2=BF2+OF2=0.82+1.52=2.89(米),
∴OA=1.7米,
∴桥洞的宽至少增加到1.7×2=3.4(米).
点评:本题考查了垂径定理和勾股定理:掌握垂直于弦的直径平分弦,并且平分弦所对的弧,建立数学模型,善于观察题目的信息是解题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
①cosα表示∠α与符号cos的乘积;
②在△ABC中,∠C=90°,则c=b•sinB;
③在直角三角形中,不论三角形的边长大小如何,如果其中一个锐角为20°不变,那么20°角的各三角函数值的大小也不变;
④在直角三角形中,锐角A的正弦值在0和1之间.
①cosα表示∠α与符号cos的乘积;
②在△ABC中,∠C=90°,则c=b•sinB;
③在直角三角形中,不论三角形的边长大小如何,如果其中一个锐角为20°不变,那么20°角的各三角函数值的大小也不变;
④在直角三角形中,锐角A的正弦值在0和1之间.
| A、①② | B、③④ | C、②③ | D、①④ |
小明在解方程x2-x=0时,只得出一个根是1,则被漏掉的一个根是( )
| A、x=0 | B、x=1 |
| C、x=2 | D、x=3 |
 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm.以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是( )| A、相离 | B、相交 | C、相切 | D、不确定 |