题目内容
13. 如图,点P是⊙O的直径AB延长线上的一点,过点P作⊙O的切线PC,切点为C,若AO=OB=PB=1,则PC的长是( )
如图,点P是⊙O的直径AB延长线上的一点,过点P作⊙O的切线PC,切点为C,若AO=OB=PB=1,则PC的长是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 连接OC,根据切线的性质可得△OPC是直角三角形,利用勾股定理即可求解.
解答  解:连接OC.
解:连接OC.
∵PC是切线,
∴OC⊥PC.
在直角△OPC中,OC=OB=1,OP=OB+PB=2.
∴PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=$\sqrt{3}$.
故选B.
点评 本题考查了切线的性质定理,已知切线常用的辅助线就是连接圆心和切线,构造直角三角形.

练习册系列答案
相关题目
3.a的平方的5倍减去3的差,应写成( )
| A. | 5a2-3 | B. | 5(a2-3) | C. | (5a)2-3 | D. | a2(5-3) |
4.下列说法中,正确的是( )
| A. | 任何有理数的绝对值都是正数 | |
| B. | 任何有理数的绝对值都不可能小于0 | |
| C. | 1是最小的正数 | |
| D. | 最大的负数是-1 |
1.下列说法:①相等的角是对顶角;②两条直线被第三条直线所截,同位角相等;③互补的两个角一定有一个为钝角,另一个角为锐角;④一个角的补角比这个角的余角大90°,其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知点P是线段AB的黄金分割点,AP>PB,若AB=2,则PB=( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | 3-$\sqrt{5}$ | D. | $\sqrt{5}$-1 |
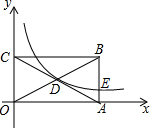 已知,矩形OABC中,BC=6,AB=4,它在平面直角坐标系中的位置如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过矩形OABC对角线的交点D.
已知,矩形OABC中,BC=6,AB=4,它在平面直角坐标系中的位置如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过矩形OABC对角线的交点D.