题目内容
13.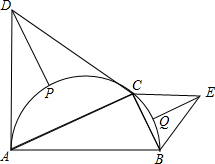 如图,C是以AB为直径的半圆O上一点.连结AC,BC,分别以AC,BC为边A外作正△ACD,正△BEC,P,Q分别是弧$\widehat{AC}$,弧$\widehat{BC}$的中点,若DP+EQ=11,AB=13,则AC+BC的长是( )
如图,C是以AB为直径的半圆O上一点.连结AC,BC,分别以AC,BC为边A外作正△ACD,正△BEC,P,Q分别是弧$\widehat{AC}$,弧$\widehat{BC}$的中点,若DP+EQ=11,AB=13,则AC+BC的长是( )| A. | 24 | B. | 12$\sqrt{3}$+12 | C. | 24$\sqrt{3}$-24 | D. | 17 |
分析 连接OP,OQ分别交AC于H,BC于I,根据垂径定理得到H、I是AC、BD的中点,根据等边三角形的性质解答即可.
解答 解:设AC+BC=x,
连接OP,OQ分别交AC于H,BC于I,
∵弧$\widehat{AC}$,弧$\widehat{BC}$的中点分别是P,Q,
∴OP⊥AC,OQ⊥BC,
∴H、I是AC、BD的中点,
∴OH+OI=$\frac{1}{2}$×(AC+BC)=$\frac{1}{2}$x,
∵AB=13,
∴OP=OI=6.5,
∴PH+QI=13-$\frac{1}{2}$x,
∵△ACD和△BEC是等边三角形,
∴DH+CI=$\frac{\sqrt{3}}{2}$x,
∴$\frac{\sqrt{3}}{2}$x-(13-$\frac{1}{2}$x)=11,
解得,x=24$\sqrt{3}$-24,
故选:C.
点评 本题考查了圆心角,弧,弦的关系,矩形的性质,等腰三角形的性质,垂径定理,中位线定理,解题的关键是正确的作出辅助线.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.下列乘法运算,不能运用乘法公式的是( )
| A. | (-x+11)(-x-11) | B. | (m+n)(-m+n) | C. | (x-7y)(7x-y) | D. | (1-30x)2 |
8.若|a|>-a,则( )
| A. | a>0 | B. | a<0 | C. | a<-1 | D. | 1<a |
18.下面的图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
 如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )| A. | a | B. | b | C. | -a | D. | -b |
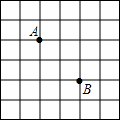 如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )
如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )