题目内容
19.已知一个平行四边形的一条对角线将其分为全等的两个等腰直角三角形,且这条对角线的长为8,则另一条对角线长为8或8$\sqrt{5}$.分析 分两种情形①平行四边形是正方形,②这个平行四边形的四个角分别为45°,135°,45°,135°.
解答 解:①当平行四边形是正方形时,满足条件,
∵一条对角线的长为8,
∴另一条对角线长为:8.
②当这个平行四边形的四个角分别为45°,135°,45°,135°.
此时另外一条对角线的长度=2•$\sqrt{{8}^{2}+{4}^{2}}$=8$\sqrt{5}$.
故另一条对角线长为8或8$\sqrt{5}$.
点评 此题主要考查了平行四边形的性质以及等腰直角三角形的性质,解题的关键是学会用分类讨论是思想思考问题,注意一题多解.

练习册系列答案
相关题目
9.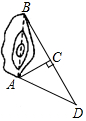 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
 如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )| A. | AAS | B. | SAS | C. | ASA | D. | SSS |
10.下列调查中,适合采用普查的是( )
| A. | 了解一批电视机的使用寿命 | |
| B. | 了解全省学生的家庭1周内丢弃塑料袋的数量 | |
| C. | 了解某校八(2)班学生每天用于课外阅读的时间 | |
| D. | 了解《最强大脑》收视率 |
14.下列说法错误的是( )
| A. | 平行于x轴的直线上的所有点的纵坐标相同 | |
| B. | 若点P(a,b)在x轴上,则a=0 | |
| C. | 平行于y轴的直线上的所有点的横坐标相同 | |
| D. | (-3,4)与(4,-3)表示两个不同的点 |
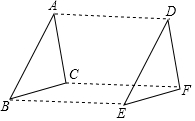 如图,△ABC经过平移后得到△DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( )
如图,△ABC经过平移后得到△DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( ) 如图,在?ABCD中,AB=5cm,AD=8cm,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=3.
如图,在?ABCD中,AB=5cm,AD=8cm,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=3.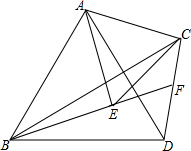 如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证:
如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证: