题目内容
10.在平顶山鹰城广场升级改造过程中,需要将如图矩形花坛改造成菱形花坛,且改造后菱形花坛面积是原矩形面积的一半,根据图中数据,求菱形花坛的边长.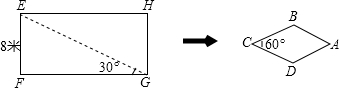
分析 设菱形边长为x米,连结AC、BD,交于O,根据菱形花坛面积是原矩形面积的一半,列出方程求解即可求解.
解答 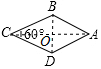 解:设菱形边长为x米,连结AC、BD,交于O,
解:设菱形边长为x米,连结AC、BD,交于O,
∵∠BCD=60°,
∴∠BCO=30°,
在Rt△BCO中,BO=$\frac{1}{2}$x,OC=$\frac{\sqrt{3}}{2}$x,
则AC=$\sqrt{3}$x,
∴菱形ABCD面积为$\frac{\sqrt{3}}{2}$x2,
∵在Rt△EFG中,∠EGF=30°,EF=8米
∴FG=8$\sqrt{3}$,
∴矩形面积为64$\sqrt{3}$,
∵菱形花坛面积是原矩形面积的一半,
∴$\frac{\sqrt{3}}{2}$x2=$\frac{1}{2}$×64$\sqrt{3}$,
解得:x1=8,x2=-8(舍去).
答:菱形花坛的边长8米.
点评 此题考查了一元二次方程的应用,菱形的性质,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
1.要使六边形木架不变形,至少要再钉上( )根木条.
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
5.某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x,则下面所列方程正确的是( )
| A. | 90(1+x)2=144 | B. | 90(1-x)2=144 | ||
| C. | 90(1+2x)=144 | D. | 90(1+x)+90(1+x)2=144-90 |
15.下列各数中,最小的数是( )
| A. | -3 | B. | |-2| | C. | (-3)2 | D. | -22 |
 如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,那么∠DEB是30°吗?说明理由.
如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,那么∠DEB是30°吗?说明理由.