题目内容
 如图,一次函数y1=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=
如图,一次函数y1=-x-1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=| k |
| x |
(1)求反比例函数的解析式;
(2)求△MOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)求出M的坐标,把M的坐标代入反比例函数的解析式,求出即可;
(2)根据M、B的坐标,结合三角形面积公式求出即可.
(2)根据M、B的坐标,结合三角形面积公式求出即可.
解答:解:(1)∵M(-2,m)在一次函数y1=-x-1的图象上,
∴代入得:m=-(-2)-1=1,
∴M的坐标是(-2,1),
把M的坐标代入y2=
得:k=-2,
即反比例函数的解析式是:y1=-
;
(2)y1=-x-1,
当x=0时,y1=-1,
即B的坐标是(0,-1),
所以OB=1,
∵M(-2,1),
∴点M到OB的距离是2,
∴△MOB的面积是
×1×2=1.
∴代入得:m=-(-2)-1=1,
∴M的坐标是(-2,1),
把M的坐标代入y2=
| k |
| x |
即反比例函数的解析式是:y1=-
| 2 |
| x |
(2)y1=-x-1,
当x=0时,y1=-1,
即B的坐标是(0,-1),
所以OB=1,
∵M(-2,1),
∴点M到OB的距离是2,
∴△MOB的面积是
| 1 |
| 2 |
点评:本题考查了一次函数和反比例函数的交点问题,三角形的面积,用待定系数法求出函数的解析式的应用,主要考查学生的推理和计算能力,题目比较好,难度适中.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
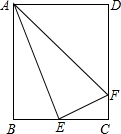 如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设
如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设| AB |
| AD |
(1)△ABE∽△ECF;(2)AE平分∠BAF;(3)当k=1时,△ABE∽△ADF;(4)tan∠EAF=k.
其中结论正确的是( )
| A、(1)(2)(3)(4) |
| B、(1)(3)(4) |
| C、(1)(2) |
| D、(2)(3) |
 如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF为( )
如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF为( )| A、55° | B、60° |
| C、75° | D、80° |
 某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.