题目内容
12.某学生化简分式$\frac{1}{x+1}$+$\frac{2}{{{x^2}-1}}$出现了错误,解答过程如下:原式=$\frac{1}{(x+1)(x-1)}$+$\frac{2}{(x+1)(x-1)}$(第一步)
=$\frac{1+2}{(x+1)(x-1)}$(第二步)
=$\frac{3}{{{x^2}-1}}$.(第三步)
(1)该学生解答过程是从第一步开始出错的,其错误原因是分式的基本性质;
(2)请写出此题正确的解答过程.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)一、分式的基本性质用错;
(2)原式=$\frac{x-1}{(x+1)(x-1)}$+$\frac{2}{(x+1)(x-1)}$
=$\frac{x+1}{(x+1)(x-1)}$
=$\frac{1}{x-1}$
故答案为:(1)一、分式的基本性质用错;
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
20. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )| A. | π | B. | 2π | C. | 4π | D. | 5π |
3.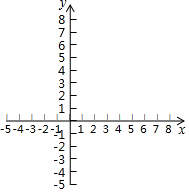 数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
(1)函数y=$\frac{x}{x+1}$的自变量x的取值范围是:x≠-1
(2)列出y与x的几组对应值,请直接写出m的值,m=3.
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数y=$\frac{x}{x+1}$的一条性质.
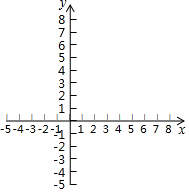 数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:(1)函数y=$\frac{x}{x+1}$的自变量x的取值范围是:x≠-1
(2)列出y与x的几组对应值,请直接写出m的值,m=3.
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
(4)结合函数的图象,写出函数y=$\frac{x}{x+1}$的一条性质.
 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D. 如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.