题目内容
在△ABC中,已知∠A=100°.
(1)如图1,若点P是∠ABC和∠ACB的平分线的交点,则∠P= .
(2)如图2,若△DEF,是由△ABC平移得到的,且∠ABC与∠DFE的平分线相交于P,求∠P的度数.
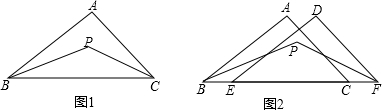
(1)如图1,若点P是∠ABC和∠ACB的平分线的交点,则∠P=
(2)如图2,若△DEF,是由△ABC平移得到的,且∠ABC与∠DFE的平分线相交于P,求∠P的度数.

考点:三角形内角和定理,三角形的外角性质,平移的性质
专题:
分析:(1)由∠A=100°.可得∠ABC+∠ACB=80°,利用角平分线的性质可得∠P=180°-
(∠ABC+∠ACB)=140°,
(2)由∠A=100°.可得∠ABC+∠ACB=80°,由△DEF是由△ABC平移得到的,利用角平分线的性质可得∠P=180°-
(∠ABC+∠DFE).
| 1 |
| 2 |
(2)由∠A=100°.可得∠ABC+∠ACB=80°,由△DEF是由△ABC平移得到的,利用角平分线的性质可得∠P=180°-
| 1 |
| 2 |
解答:解:(1)如图1,
∵∠A=100°.
∴∠ABC+∠ACB=80°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-
(∠ABC+∠ACB)=180°-
×80°=140°,
故答案为:140°.
(2)如图2,
∵∠A=100°.
∴∠ABC+∠ACB=80°,
∵△DEF,是由△ABC平移得到的,
∴∠ABC+∠DFE=80°,
∵点P是∠ABC和∠DFE的平分线的交点,
∴∠P=180°-
(∠ABC+∠DFE)=180°-
×80°=140°,
∵∠A=100°.
∴∠ABC+∠ACB=80°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:140°.
(2)如图2,
∵∠A=100°.
∴∠ABC+∠ACB=80°,
∵△DEF,是由△ABC平移得到的,
∴∠ABC+∠DFE=80°,
∵点P是∠ABC和∠DFE的平分线的交点,
∴∠P=180°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了三角形内角和定理及平移的性质,解题的关键是利用三角形内角和定理得∠ABC+∠ACB=80°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
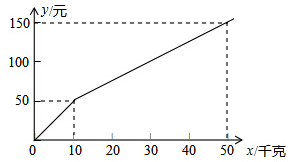 某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示
某种子公司以一定的价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不包含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(元)与一次购买种子数量x(千克)之间的函数关系如图所示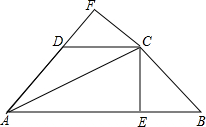 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,