题目内容
19．为了求1+3+32+33+…+3100的值，可令M=1+3+32+33+…+3100，则3M=3+32+33+34+…+3101，因此，3M-M=3101-1，所以M=$\frac{{3}^{101}-1}{2}$，即1+3+32+33+…+3100=$\frac{{3}^{101}-1}{2}$，仿照以上推理计算：1+5+52+53+…+52015的值是$\frac{{5}^{2016}-1}{4}$．分析 根据题目信息，设M=1+5+52+53+…+52015，求出5M，然后相减计算即可得解．
解答 解：设M=1+5+52+53+…+52015，
则5M=5+52+53+54…+52016，
两式相减得：4M=52016-1，
则M=$\frac{{5}^{2016}-1}{4}$．
故答案为$\frac{{5}^{2016}-1}{4}$．
点评 本题考查了有理数的乘方，读懂题目信息，理解求和的运算方法是解题的关键．
练习册系列答案
相关题目
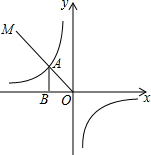如图所示，第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于点A，已知OA=3$\sqrt{2}$，则k=-9．
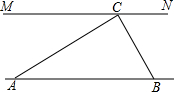为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，结果保留整数）
14．下列说法正确的是（ ）
| A． | 面积相等的两个三角形全等 | |
| B． | 矩形的四条边一定相等 | |
| C． | 一个图形和它旋转后所得图形的对应线段相等 | |
| D． | 随机投掷一枚质地均匀的硬币，落地后一定是正面朝上 |
11．函数y=$\frac{\sqrt{x+3}}{x-5}$中自变量x的取值范围是（ ）
| A． | x≥-3 | B． | x≠5 | C． | x≥-3或x≠5 | D． | x≥-3且x≠5 |
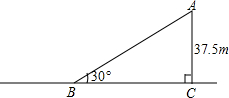一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下，速度每秒增加1.5m/s，已知斜坡高37.5m，坡角为30°．
