题目内容
阅读材料:如果方程x2+px+q=0的两个根是x1,x2,那么x1+x2=-p; x1x2=q,请根据以上结论,解决下列问题:
(1)已知x1,x2是方程x-4x+2=0的两根,求:
①x12+x22的值;②
+
的值.
(2)已知a,b满足a2-15a-5=0,b2-15b-5=0,求
+
的值.
(1)已知x1,x2是方程x-4x+2=0的两根,求:
①x12+x22的值;②
| 1 |
| x1 |
| 1 |
| x2 |
(2)已知a,b满足a2-15a-5=0,b2-15b-5=0,求
| a |
| b |
| b |
| a |
考点:根与系数的关系
专题:阅读型
分析:(1)根据x1,x2是方程x-4x+2=0的两根,得出x1+x2=4; x1x2=2,再把x12+x22变形为(x1+x2)2-2x1x2,把
+
变形为
,然后代入计算即可;
(2)根据a,b满足a2-15a-5=0,b2-15b-5=0,得出a,b是x2-15x-5=0的根,分①当a≠b时;②当a=b时;求出a+b与ab的值,再把要求的式子
+
进行变形,然后代入计算即可.
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
(2)根据a,b满足a2-15a-5=0,b2-15b-5=0,得出a,b是x2-15x-5=0的根,分①当a≠b时;②当a=b时;求出a+b与ab的值,再把要求的式子
| a |
| b |
| b |
| a |
解答:解:(1)∵x1,x2是方程x-4x+2=0的两根,
∴x1+x2=4; x1x2=2,
∴①x12+x22=(x1+x2)2-2x1x2=42-2×2=12;
②
+
=
=
=2;
(2)∵a,b满足a2-15a-5=0,b2-15b-5=0,
∴a,b是x2-15x-5=0的根,
∴①当a≠b时,a+b=15,ab=-5,
∴
+
=
=
=
=-47;
②当a=b时,原式=2.
∴x1+x2=4; x1x2=2,
∴①x12+x22=(x1+x2)2-2x1x2=42-2×2=12;
②
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 4 |
| 2 |
(2)∵a,b满足a2-15a-5=0,b2-15b-5=0,
∴a,b是x2-15x-5=0的根,
∴①当a≠b时,a+b=15,ab=-5,
∴
| a |
| b |
| b |
| a |
| a2+b2 |
| ab |
| (a+b)2-2ab |
| ab |
| 152-2×(-5) |
| -5 |
②当a=b时,原式=2.
点评:此题考查了根与系数的关系,关键是熟知一元二次方程根与系数的关系:x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列式子中,是二次根式的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
-4
与
的差的绝对值与-5的和是( )
| 1 |
| 3 |
| 2 |
| 3 |
| A、-10 | ||
| B、10 | ||
| C、0 | ||
D、-10
|
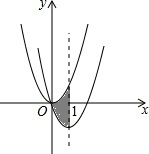 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( )
如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( ) 如图所示的某种计算装置,当输入的数为x,输出的数为y,小明经过尝试,得到下表的数据:
如图所示的某种计算装置,当输入的数为x,输出的数为y,小明经过尝试,得到下表的数据: 如图,△ABC≌△DEF,△DEF周长是26cm,DE=9cm,EF=11cm,∠E=∠B,则AC=
如图,△ABC≌△DEF,△DEF周长是26cm,DE=9cm,EF=11cm,∠E=∠B,则AC=