题目内容
在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了36次手,则参加这次聚会的有多少人?设有x人,列方程为( )
| A、x(x-1)=36 | ||
| B、x(x+1)=36 | ||
C、
| ||
D、
|
考点:由实际问题抽象出一元二次方程
专题:
分析:每个人都要和他自己以外的人握手一次,但两个人之间只握手一次,所以等量关系为:
×聚会人数×(聚会人数-1)=总握手次数,把相关数值代入即可求解.
| 1 |
| 2 |
解答:解:参加聚会的人数为x名,每个人都要握手(x-1)次,
∴可列方程为
x(x-1)=36.
故选D.
∴可列方程为
| 1 |
| 2 |
故选D.
点评:本题考查用一元二次方程解决握手次数问题,得到总次数的等量关系是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
用配方法解方程x2-6x+4=0时,配方后得的方程为( )
| A、(x+3)2=5 |
| B、(x-3)2=-13 |
| C、(x-3)2=5 |
| D、(x-3)2=13 |
 如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )
如图,△ABC≌△BAD,如果AB=6cm,BD=4cm,AD=5cm,那么BC的长是( )| A、4cm | B、5cm |
| C、6cm | D、无法确定 |
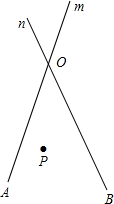 如图,直线m和n相交于点O,
如图,直线m和n相交于点O, 根据图示,用代数式表示出阴影部分的面积
根据图示,用代数式表示出阴影部分的面积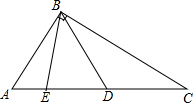 如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.
如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.