题目内容
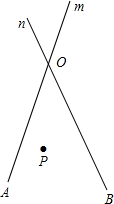 如图,直线m和n相交于点O,
如图,直线m和n相交于点O,(1)分别画出点P关于直线m、n的对称点P1、P2;
(2)若直线m、n相交的锐角∠AOB=50°,求∠P1OP2的度数;
(3)若OP=4,P1P2=6,求△P1OP2的周长.
考点:作图-轴对称变换
专题:
分析:(1)过点P作PP1⊥m并且被m平分,作PP2⊥n并且被n平分,即可得解;
(2)根据轴对称的性质可得∠P1OA=∠POA,∠P2OB=∠POB,然后求出∠P1OP2=2∠AOB,代入数据计算即可得解;
(3)根据轴对称的性质可得OP1=OP2=OP,再根据三角形的周长的定义列式计算即可得解.
(2)根据轴对称的性质可得∠P1OA=∠POA,∠P2OB=∠POB,然后求出∠P1OP2=2∠AOB,代入数据计算即可得解;
(3)根据轴对称的性质可得OP1=OP2=OP,再根据三角形的周长的定义列式计算即可得解.
解答: 解:(1)点P1、P2如图所示;
解:(1)点P1、P2如图所示;
(2)∵点P关于直线m、n的对称点P1、P2,
∴∠P1OA=∠POA,∠P2OB=∠POB,
∴∠P1OP2=∠P1OA+∠POA+∠P2OB+∠POB=2∠AOB,
∵∠AOB=50°,
∴∠P1OP2=2×50°=100°;
(3)∵点P关于直线m、n的对称点P1、P2,
∴OP1=OP2=OP=4,
∴△P1OP2的周长=4+4+6=14.
 解:(1)点P1、P2如图所示;
解:(1)点P1、P2如图所示;(2)∵点P关于直线m、n的对称点P1、P2,
∴∠P1OA=∠POA,∠P2OB=∠POB,
∴∠P1OP2=∠P1OA+∠POA+∠P2OB+∠POB=2∠AOB,
∵∠AOB=50°,
∴∠P1OP2=2×50°=100°;
(3)∵点P关于直线m、n的对称点P1、P2,
∴OP1=OP2=OP=4,
∴△P1OP2的周长=4+4+6=14.
点评:本题考查了利用轴对称变换作图,轴对称的性质,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x2-2x-1=0的两个解为x1和x2,则x1+x2的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
 如图,点E在正方形ABCD的边BC的延长线上,且BE=BD,则∠E的度数为( )
如图,点E在正方形ABCD的边BC的延长线上,且BE=BD,则∠E的度数为( )| A、45° | B、60° |
| C、67.5° | D、75° |
关于x的一元二次方程2x2+x-k=0有实数根,则k的取值范围是( )
A、k<
| ||
B、k>
| ||
C、k≤
| ||
D、k≥-
|
在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了36次手,则参加这次聚会的有多少人?设有x人,列方程为( )
| A、x(x-1)=36 | ||
| B、x(x+1)=36 | ||
C、
| ||
D、
|