题目内容
17.若(x2+nx+3)(x2-3x+m)展开式中不含x2和x3项,求(n-m)n的值.分析 先根据多项式乘以多项式法则展开,合并后得出方程组,求出方程组的解,最后代入求出即可.
解答 解:(x2+nx+3)(x2-3x+m)
=x4-3x3+mx2+nx3-3nx2+mnx+3x2-9x+3m
=x4+(n-3)x3+(m-3n+3)x2+(mn-9)x+3m,
∵展开式中不含x2,x3项,
∴$\left\{\begin{array}{l}n-3=0\\ m-3n+3=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}m=6\\ n=3\end{array}\right.$,
当m=6,n=3时(n-m)n
=(3-6)3
=(-3)3
=-27.
点评 本题考查了多项式乘以多项式法则,解二元一次方程组,求出代数式的值的应用,能求出m、n的值是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:如图所示,
已知:如图所示,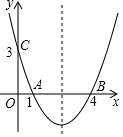 如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.
如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.