题目内容
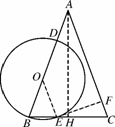
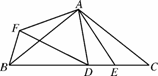
已知:如图N19,在△ABC中,AB=AC=6,cosB=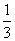 ,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.
,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)设OB=x,CF=y.
①求y关于x的函数关系式;
②当直线DF与⊙O相切时,求OB的长.
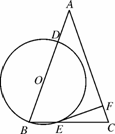
图N19
解:(1)直线EF与⊙O相切.理由如下:
如图104(1),连接OE,
则OE=OB,∠OBE=∠OEB.
∵AB=AC,∴∠OBE=∠C,∴∠OEB=∠C.
∴OE∥AC.∵EF⊥AC,∴EF⊥OE.
∵点E在⊙O上,∴直线EF与⊙O相切.
(2)①如图104(1),作AH⊥BC,H为垂足,
那么BH=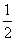 BC.
BC.
∵AB=6,cosB=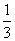 ,∴BH=2,BC=4.
,∴BH=2,BC=4.
∵OE∥AC,∴△BOE∽△BAC.
∴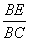 =
=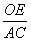 ,即
,即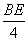 =
=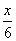 ,
,
∴BE=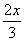 .∴EC=4-
.∴EC=4-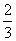 x.
x.
在Rt△ECF中,cosC=cos B=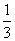 ,
,
∴CF=EC·cosC=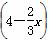 ×
×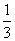 ,
,
∴所求函数的关系式为y=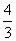 -
-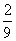 x.
x.
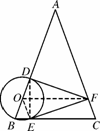
(1) (2)
图104
②如图104(2),连接OE,DE,OF,
由EF,DF与⊙O相切,
∴FD=FE,且∠DFO=∠EFO,
则OF垂直平分DE.
由∠DEB=90°,∴BC⊥DE.
∴OF∥BC,则四边形OBCF是等腰梯形.
∴OB=CF,得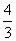 -
-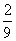 x=x,
x=x,
解得x=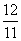 ,即OB=
,即OB=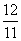 .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,
, 是同一个反比例函数图象上的两点.若
是同一个反比例函数图象上的两点.若 ,且
,且 ,则这个反比例函数的表达式为 .
,则这个反比例函数的表达式为 .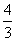 ,则sinα的值为( )
,则sinα的值为( )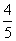 B.
B. 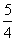 C.
C. 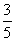 D.
D.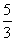
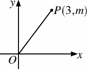


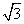 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.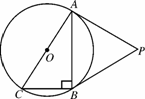
 C、
C、 D、
D、