题目内容
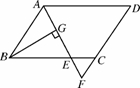
已知:如图N38,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2 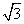 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
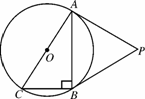
(1)证明:连接OB,
∴OA=OB,PA=PB.
∴∠OAB=∠OBA,∠PAB=∠PBA.
∴∠PAO=∠PBO.
又∵PA是⊙O的切线,∴∠PAO=90°.
∴∠PBO=90°,∴OB⊥PB.
又∵OB是⊙O的半径,∴PB是⊙O的切线.
(2)解:连接OP,交AB于点D.
∵PA=PB,OA=OB,
∴点P和点O都在线段AB的垂直平分线上.
∴OP垂直平分线段AB.∴AD=BD.
∵OA=OC,∴OD=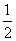 BC=1.
BC=1.
∵∠PAO=∠PDA=90°,∠AOP=∠DAP,
∴△APO∽△DPA.
∴ =
=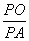 .∴AP2=PO·DP.
.∴AP2=PO·DP.
∴PO(PO-OD)=AP2.
即PO2-1×PO=(2 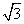 )2,解得PO=4.
)2,解得PO=4.
在Rt△APO中,OA=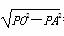 =2,
=2,
即⊙O的半径为2.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
在篮球比赛中,某队员连续10场比赛中每场的得分情况如下表所示:
| 场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 38 |
则这10场比赛中他得分的中位数和众数分别是( )
A.10,4 B.10,7 C.7,13 D.13,4
 ,如果
,如果 ,那么
,那么 (填“>”、“=”、“<”)。
(填“>”、“=”、“<”)。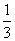 ,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.
,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.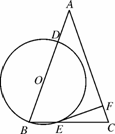





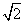 ,则△EFC的周长为________.
,则△EFC的周长为________.