题目内容
10.如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.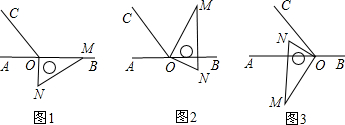
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM=120度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是6或24秒.
分析 (1)根据OM恰好平分∠BOC,用∠BOC的度数除以2,求出∠BOM的度数,即可求出∠AOM的度数是多少.
(2)首先根据∠AOM-∠NOC=30°,∠BOC=120°,求出∠A0C=60°,然后根据∠AON=90°-∠AOM=60°-∠NOC,判断出∠AOM与∠NOC之间满足什么等量关系即可.
(3)首先设三角板绕点O旋转的时间是x秒,根据∠BOC=120°,可得∠AOC=60°,∠BON=∠COD=30°;然后根据旋转60°时ON平分∠AOC,可得10x=60或10x=240,据此求出x的值是多少即可.
解答 解:(1)∵OM恰好平分∠BOC,
∴∠BOM=120°÷2=60°,
∴∠AOM=180°-120°=60°.
(2)如图3,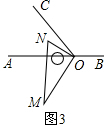 ,
,
∠AOM-∠NOC=30°,
∵∠BOC=120°,
∴∠A0C=60°,
∵∠AON=90°-∠AOM=60°-∠NOC,
∴∠AOM-∠NOC=30°.
(3)设三角板绕点O旋转的时间是x秒,
∵∠BOC=120°,
∴∠AOC=60°,
∴∠BON=∠COD=30°,
∴旋转60°时ON平分∠AOC,
∵10x=60或10x=240,
∴x=6或x=24,
即此时三角板绕点O旋转的时间是6或24秒.
故答案为:120、6或24.
点评 此题主要考查了角的计算,考查了分类讨论思想的应用,以及角平分线的性质和应用,要熟练掌握.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18. 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )| A. | 4cm | B. | 5cm | C. | 8cm | D. | 9cm |
15.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{15}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{12}}$ |
19.若x=1是一元二次方程(x+1)2-a(x+1)-2=0的一个根,则a的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
20.下列函数中,是一次函数但不是正比例函数的是( )
| A. | y=2x | B. | y=$\frac{1}{x}$+2 | C. | y=$\frac{1}{3}$-$\frac{1}{2}$x | D. | y=2x2-1 |
 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.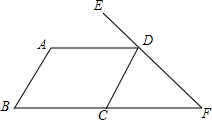 如图,∠A=120°,∠B=60°,∠EDA=55°,则∠F=55度.
如图,∠A=120°,∠B=60°,∠EDA=55°,则∠F=55度.