题目内容
16.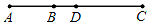 如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话:
如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话:(1)图形中共有6条线段.
(2)若AB=2 cm,求BD的长.
解:∵AB=2 cm,BC=2AB,
∴BC=4 cm
∴AC=AB+BC=6cm
∵D是AC的中点,
∴AD=$\frac{1}{2}$AC=3cm.(中点定义)
∴BD=AD-AB=1cm.
分析 (1)结合图形得出所有线段即可得;
(2)求出BC长,根据线段中点求出AD,代入BD=AD-AB求出即可.
解答 解:(1)图形中共有AB、AD、AC、BD、BC、DC这6条线段,
故答案为:6.
(2)∵AB=2 cm,BC=2AB,
∴BC=4 cm
∴AC=AB+BC=6cm
∵D是AC的中点,
∴AD=$\frac{1}{2}$AC=3cm.(中点定义)
∴BD=AD-AB=1cm,
故答案为:BC、6、AC、3、AB、1.
点评 本题考查了线段中点和求两点间的距离的应用,关键是求出AC、AD长和得出BD=AD-AB.

练习册系列答案
相关题目
13.要使分式$\frac{x+2}{x-3}$有意义,x的取值应满足( )
| A. | x≠-2 | B. | x≠3 | C. | x≠-2且x≠3 | D. | x≠-2或x≠3 |
11.点A、B、C是直线n上的三点,P是直线n外一点,PA=12,PB=8,PC=9,则P到直线n的距离( )
| A. | 不大于8 | B. | 大于8小于9 | C. | 大于9小于12 | D. | 总是8 |
 如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm.
如图,将一根绳子对折以后用线段AB表示,点P是AB的四等分点,现从P处将绳子剪断,剪断后的各段绳子中的一段长为30cm,则这条绳子的原长为40或80或120或240cm. 在湖的两侧有A,B两个消防栓,为测定它们之间的距离,小明在岸上任选一点C,并量取了AC中点D和BC中点E之间的距离为16米,则A,B之间的距离应为32 米.
在湖的两侧有A,B两个消防栓,为测定它们之间的距离,小明在岸上任选一点C,并量取了AC中点D和BC中点E之间的距离为16米,则A,B之间的距离应为32 米.