题目内容
12.在等腰直角三角形中,斜边长为50cm,则它的面积为625cm2.分析 设等腰直角三角形的直角边长为acm,由勾股定理得出方程,解方程求出a2,等腰直角三角形的面积=$\frac{1}{2}$a2,即可得出结果.
解答 解:设等腰直角三角形的直角边长为acm,
则a2+a2=502,
解得:a2=1250,
∴等腰直角三角形的面积=$\frac{1}{2}$a2=$\frac{1}{2}$×1250=625(cm2),
故答案为:625cm2.
点评 本题考查了等腰直角三角形的性质、勾股定理、等腰直角三角形面积的计算;熟练掌握等腰直角三角形的性质,运用勾股定理求出直角边长的平方是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.将甲、乙、丙三人随机地分到高一(1)班和高一(2)班去,甲、乙同班的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
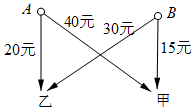 我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.
我县黄泛区农场有A、B两个果园,分别收获水果380件,320件,现需把这些水果全部运往甲、乙两个销售点,每件运费如图所示.现甲销售点需水果400件,乙销售点需水果300件.
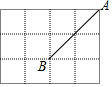 如图,在4×3的正方形网格中,点A、B分别在格点上,在图中确定格点C,则以A、B、C为顶点的等腰三角形有3个.
如图,在4×3的正方形网格中,点A、B分别在格点上,在图中确定格点C,则以A、B、C为顶点的等腰三角形有3个.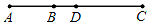 如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话:
如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点.看图说话: