题目内容
5.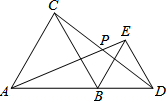 如图,点A,B,D在同一直线上,△ABC和△BDE都是等边三角形,连接AE,CD相交于点P,则∠CPE的度数为120度.
如图,点A,B,D在同一直线上,△ABC和△BDE都是等边三角形,连接AE,CD相交于点P,则∠CPE的度数为120度.
分析 由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而可得出结论.
解答 解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
在△ABE与△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠CBD}\\{BD=BE}\end{array}\right.$,
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
∵∠AEB+∠EAB=60°,
∴∠ADP+∠EAD=60°,
∴∠CPE=∠APB=180°-(∠PAD+∠PDA)=120°,
故答案为:120°.
点评 本题主要考查了等边三角形的性质及全等三角形的判定及性质问题,能够熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若直角三角形的三边长分别为a-b、a、a+b,且a、b都是正整数,则三角形其中一边的长可能为( )
| A. | 22 | B. | 32 | C. | 62 | D. | 82 |
10.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当∠B=90°时(如图甲),测得对角线BD的长为$\sqrt{2}$.当∠B=60°时(如图乙),则对角线BD的长为( )
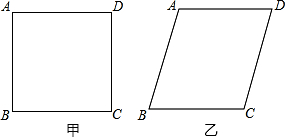

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
14.下列各式计算正确的是( )
| A. | a2+3a2=4a4 | B. | 3a3•2a2=6a6 | C. | a5÷a=a4 | D. | -2-2=$\frac{1}{4}$ |
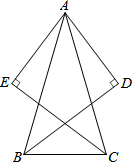 如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.
如图,△ABC为等腰三角形,AB=AC,BD分别平分∠ABC,CE分别平分∠ACB,过点A分别作BD、CE的垂线段,垂足为D、E.求证:AD=AE.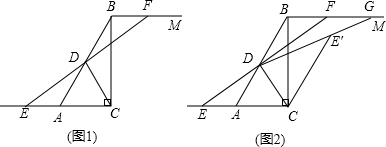
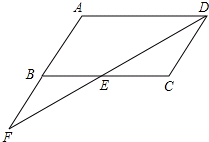 已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.
已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.