题目内容
19. 如图,有一个用木条钉成的平行四边形玩具,对角线AC,BD之间用抻直的皮筋连接,已知AB=1,BC=$\sqrt{3}$,若推动这个玩具,当∠ABC=90°时,皮筋BD长是( )
如图,有一个用木条钉成的平行四边形玩具,对角线AC,BD之间用抻直的皮筋连接,已知AB=1,BC=$\sqrt{3}$,若推动这个玩具,当∠ABC=90°时,皮筋BD长是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 证出四边形ABCD是矩形,由矩形的性质得出BD=AC,再由勾股定理求出AC即可.
解答 解:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴BD=AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2;
故选:B.
点评 此题主要考查了矩形的判定以及平行四边形的性质、勾股定理;证明四边形ABCD是矩形是解题关键.

练习册系列答案
相关题目
10.下列图形即是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
7.若点P(2a-8,2-a)在第三象限内,且a为整数,则a的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.下列小数都是无限小数,其中不是循环小数的是( )
| A. | 11223344… | B. | 2.231231231231… | ||
| C. | 0.1428142814281428… | D. | 0.1111111… |
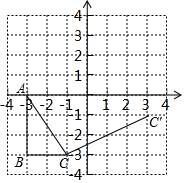 如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3)
如图,在平面直角坐标系中,Rt△ABC的三个顶点坐标为A(-3,0),B(-3,-3),C(-1,-3)
 如图,点A,B,C在⊙O上,∠ABO=65°,则∠ACB的度数是25度.
如图,点A,B,C在⊙O上,∠ABO=65°,则∠ACB的度数是25度.