题目内容
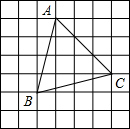 如图,方格纸中小正方形的边长为1,△ABC是格点三角形.
如图,方格纸中小正方形的边长为1,△ABC是格点三角形.(1)求证:△ABC是等腰三角形;
(2)求AC边上的高.
考点:勾股定理,等腰三角形的判定
专题:网格型
分析:(1)根据勾股定理求出AB、BC、AC的长,再根据等腰三角形的判定判断即可;
(2)过B作BD⊥AC于D,根据等腰三角形的性质求出AD,根据勾股定理求出BD即可.
(2)过B作BD⊥AC于D,根据等腰三角形的性质求出AD,根据勾股定理求出BD即可.
解答:(1)证明:∵方格纸中小正方形的边长为1,
∴小正方形的边长为1,
∵由勾股定理得:AC2=32+32=18,BC2=12+42=17,AB2=12+42=17,
∴AC=
=3
,BC=
,AB=
,
∴BC=AB,
即△ABC是等腰三角形;
(2)解:过B作BD⊥AC于D,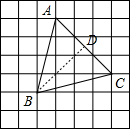
∵BC=AB,
∴AD=CD=
AC=
,
在Rt△ADB中,由勾股定理得:BD=
=
=
,
即AC边上的高是
.
∴小正方形的边长为1,
∵由勾股定理得:AC2=32+32=18,BC2=12+42=17,AB2=12+42=17,
∴AC=
| 18 |
| 2 |
| 17 |
| 17 |
∴BC=AB,
即△ABC是等腰三角形;
(2)解:过B作BD⊥AC于D,

∵BC=AB,
∴AD=CD=
| 1 |
| 2 |
3
| ||
| 2 |
在Rt△ADB中,由勾股定理得:BD=
| AB2-AD2 |
(
|
5
| ||
| 2 |
即AC边上的高是
5
| ||
| 2 |
点评:本题考查了勾股定理,等腰三角形的性质和判定的应用,能根据勾股定理求出各个边的长是解此题的关键,难度适中.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数. 已知△ABC,过点C作AB边上的高线CD,过点A作BC边上的高线AE.
已知△ABC,过点C作AB边上的高线CD,过点A作BC边上的高线AE. 如图所示,球体状容器的半径为R(R为常数),当液面高度为h时,水平液面面积A的函数表达式为
如图所示,球体状容器的半径为R(R为常数),当液面高度为h时,水平液面面积A的函数表达式为 如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上
如图,AB是⊙O的直径,弦CD⊥AB于点N,点M在⊙O上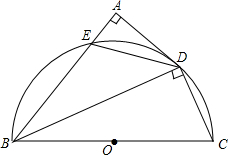 如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4
如图,BC为半圆的直径,O为圆心,BC=10,AD与半圆相切于点D,AB交⊙O于点E,DA⊥AB,AD=4