题目内容
方程组
有正整数解,求整数m的值.
|
考点:二元一次方程组的解
专题:
分析:先把m当作已知求出x、y的值,再根据方程组有正整数解,得到关于m的一元一次不等式组,求出m的取值范围,再找出符合条件的正整数m的值即可.
解答:解:
,
①-②×2得:
y=
,
将y=
代入②,得:
x=
,
∵方程组有正解,
∴
,
解得:m>-4,
∵方程组有正整数解,
∴m+4=1或2或3或6,
即:m=-3或-2或-1或2.
|
①-②×2得:
y=
| 6 |
| m+4 |
将y=
| 6 |
| m+4 |
x=
| 12 |
| m+4 |
∵方程组有正解,
∴
|
解得:m>-4,
∵方程组有正整数解,
∴m+4=1或2或3或6,
即:m=-3或-2或-1或2.
点评:本题考查的是解二元一次方程组及解二元一次不等式组,解答此题的关键是先把m当作已知表示出x、y的值,再根据方程组有正整数解得出关于m的不等式组,求出m的正整数解即可.

练习册系列答案
相关题目
 如图:PA、PC分别是△ABC外角∠MAC与∠NCA的平分线,并交于点P,PD⊥BM于点D,PF⊥BN于点F.
如图:PA、PC分别是△ABC外角∠MAC与∠NCA的平分线,并交于点P,PD⊥BM于点D,PF⊥BN于点F. 如图,在矩形ABCD中,点F在CB的延长线上,AE=EF,CF=CA,求证:BE⊥DE.
如图,在矩形ABCD中,点F在CB的延长线上,AE=EF,CF=CA,求证:BE⊥DE.

 如图,AC,BD相交于点O,∠AOB=∠A,∠COD=∠D,试问:∠A与∠D之间的大小有什么关系?并说明理由.
如图,AC,BD相交于点O,∠AOB=∠A,∠COD=∠D,试问:∠A与∠D之间的大小有什么关系?并说明理由.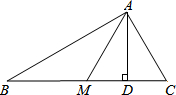 已知AM是△ABC的中线.
已知AM是△ABC的中线.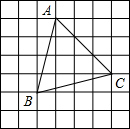 如图,方格纸中小正方形的边长为1,△ABC是格点三角形.
如图,方格纸中小正方形的边长为1,△ABC是格点三角形.