题目内容
10. 甲、乙两台机器共加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示.
甲、乙两台机器共加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示.(1)甲机器改变工作效率前每小时加工零件20个.
(2)求乙机器改变工作效率后y与x之间的函数关系式,并求出自变量x的取值范围.
(3)求这批零件的总个数.
(4)直接写出当甲、乙两台机器所加工零件数相差10个时,x的值为$\frac{1}{2},\frac{9}{2},\frac{11}{2}$.
分析 (1)甲改变工作效率前的工作效率为改变前加工的总件数,除以加工的总时间即可;
(2)利用待定系数法求一次函数解析式即可;
(3)利用函数解析式求出甲、乙两机器6小时加工的总件数,求其和即可;
(4)根据题意列方程即可得到结论.
解答 解:(1)80÷4=20(件),
故答案为:20;
(2)∵图象过C(2,80),D(5,110),
∴设解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{2k+b=80}\\{5k+b=110}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=10}\\{b=60}\end{array}\right.$,
∴y乙=10x+60(2≤x≤6);
(3)∵AB过(4,80),(5,110),
∴设AB的解析式为y甲=mx+n(m≠0),
∴$\left\{\begin{array}{l}{4m+n=80}\\{5m+n=110}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=30}\\{n=-40}\end{array}\right.$,
∴y甲=30x-40(4≤x≤6),
当x=6时,y甲=30×6-40=140,y乙=10×6+60=120,
∴这批零件的总个数是140+120=260;
(4)40x-10=20x,
解得:x=$\frac{1}{2}$,
10x+60-10=30x-40,
解得:x=$\frac{9}{2}$,
30x-40-10=10x+60,
解得:x=$\frac{11}{2}$,
当甲、乙两台机器所加工零件数相差10个时,x的值为$\frac{1}{2},\frac{9}{2},\frac{11}{2}$,
故答案为:$\frac{1}{2},\frac{9}{2},\frac{11}{2}$.
点评 此题主要考查了一次函数的应用,根据题意得出函数关系式以及数形结合是解决问题的关键.

| A. | 3x+1=2x-1 | B. | 3x-1=2x+1 | C. | 3x+2x-2=0 | D. | 3x+2x+2=0 |
| A. | $\frac{2400}{x}$=$\frac{2400+30}{x+3}$ | B. | $\frac{2400+30}{x}$=$\frac{2400}{x-3}$ | ||
| C. | $\frac{2400-30}{x-3}$=$\frac{2400}{x}$ | D. | $\frac{2400-30}{x}$=$\frac{2400}{x-3}$ |
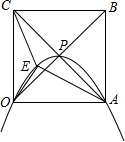 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.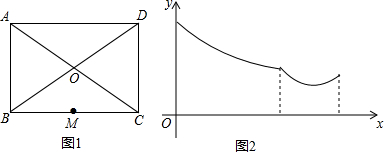
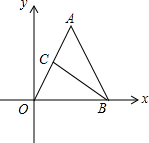 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限,点B在x轴正半轴上,AO=AB,OB=4,tan∠AOB=2,点C是线段OA的中点. 如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.
如图,OA,OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为70°.