题目内容
1.若方程组$\left\{\begin{array}{l}{ax-2y=1}\\{ax+2y=5}\end{array}\right.$的解满足条件x=y,则a=3.分析 先把两式相减求得y的值,根据x=y得到x的值,再代入任意一个方程即可求出a的值.
解答 解:$\left\{\begin{array}{l}{ax-2y=1①}\\{ax+2y=5②}\end{array}\right.$,
②-①得4y=4,
解得y=1,
∵x=y,
∴x=1,
把x=y=1代入①得a-2=1,
解得a=3.
故答案为:3.
点评 本题考查的是二元一次方程组的解,先根据题意求出x和y的值是解答此题的关键.

练习册系列答案
相关题目
12.做大小两个纸盒,尺规如下(单位:cm)
(1)做这两个纸盒共用料多少平方厘米?(结果用含a、b、c的代数式表示)
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
| 长 | 宽 | 高 | |
| 小纸盒 | a | b | c |
| 大纸盒 | 3a | 2b | 2c |
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
13. 如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
 如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )| A. | 165° | B. | 135° | C. | 125° | D. | 115° |
10. 某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:
某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:
测试成绩频数分布表
(1)填空:a=4,b=32%,本次跳绳测试成绩的中位数落在C组(请填写字母);
(2)补全频数分布直方图;
(3)已知本班中甲、乙两位同学的测试成绩分别为185次、195次,现要从E组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中至少1人被选中的概率.
 某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:
某数学兴趣小组将我校九年级某班学生一分钟跳绳的测试成绩进行了整理,分成5个小组(x表成绩,单位:次,且100≤x<200),根据测试成绩绘制出部分频数分布表和部分频数分布直方图,其中B、E两组测试成绩人数直方图的高度比为4:1,请结合下列图标中相关数据回答下列问题:测试成绩频数分布表
| 组别 | 成绩x次 | 频数(人数) | 频率 |
| A | 100≤x<120 | 5 | |
| B | 120≤x<140 | b | |
| C | 140≤x<160 | 15 | 30% |
| D | 160≤x<180 | 10 | |
| E | 180≤x<200 | a |
(2)补全频数分布直方图;
(3)已知本班中甲、乙两位同学的测试成绩分别为185次、195次,现要从E组中随机选取2人介绍经验,请用列表法或画树状图的方法,求出甲、乙两人中至少1人被选中的概率.
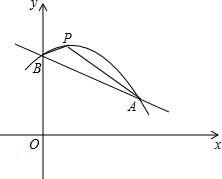 如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点.
如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点. 如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.