题目内容
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).
(1)求售价与利润的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(1)求售价与利润的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
考点:二次函数的应用
专题:
分析:(1)根据题意可知y与x的函数关系式.
(2)根据题意可知y=-10-(x-5.5)2+2402.5,当x=5.5时y有最大值.
(2)根据题意可知y=-10-(x-5.5)2+2402.5,当x=5.5时y有最大值.
解答:解:(1)由题意得:y=(210-10x)(50+x-40)=-10x2+110x+2100(0<x≤15且x为整数);
(2)由(1)中的y与x的解析式配方得:y=-10(x-5.5)2+2402.5.
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元),
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
(2)由(1)中的y与x的解析式配方得:y=-10(x-5.5)2+2402.5.
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元),
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
点评:此题主要考查了二次函数的应用以及二次函数的最值问题,根据每天的利润=一件的利润×销售量,建立函数关系式,借助二次函数解决实际问题是解题关键.

练习册系列答案
相关题目
网上购物已成为现代人消费的新趋势,2014年天猫“11•11”购物狂欢节创造了一天571亿元的支付宝成交额,其中571亿用科学记数法表示为( )
| A、5.71×102 |
| B、571×108 |
| C、5.71×1010 |
| D、0.571×1011 |
 如图,平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中有平行四边形( )
如图,平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中有平行四边形( )| A、4个 | B、5个 | C、8个 | D、9个 |

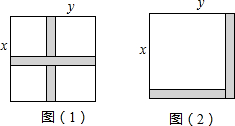 如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.
如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.