题目内容
计算下列各题:
(1)(-2x3y)2•(-xy2);
(2)(a+3)(a-1)-a(a-2);
(3)(2x+y)2-(2x+3y)(2x-3y);
(4)(x+y)(x-y)-(4x3y-8xy3)÷2xy.
(1)(-2x3y)2•(-xy2);
(2)(a+3)(a-1)-a(a-2);
(3)(2x+y)2-(2x+3y)(2x-3y);
(4)(x+y)(x-y)-(4x3y-8xy3)÷2xy.
考点:整式的混合运算
专题:计算题
分析:(1)原式先计算乘方运算,再计算乘法运算即可得到结果;
(2)原式第一项利用多项式乘以多项式法则计算,第二项利用单项式乘以多项式法则计算,去括号合并即可得到结果;
(3)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可得到结果;
(4)原式第一项利用平方差公式化简,第二项利用多项式除以单项式法则计算即可得到结果.
(2)原式第一项利用多项式乘以多项式法则计算,第二项利用单项式乘以多项式法则计算,去括号合并即可得到结果;
(3)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可得到结果;
(4)原式第一项利用平方差公式化简,第二项利用多项式除以单项式法则计算即可得到结果.
解答:解:(1)原式=4x6y2•(-xy2)=-4x7y4;
(2)原式=(a2+2a-3)-(a2-2a)=a2+2a-3-a2+2a=4a-3;
(3)原式=(4x2+4xy+y2)-(4x2-9y2)=4x2+4xy+y2-4x2+9y2=4xy+10y2;
(4)原式=(x2-y2)-(4x3y÷2xy)-(-8xy3÷2xy)=x2-y2-2x2+4y2=-x2+3y2.
(2)原式=(a2+2a-3)-(a2-2a)=a2+2a-3-a2+2a=4a-3;
(3)原式=(4x2+4xy+y2)-(4x2-9y2)=4x2+4xy+y2-4x2+9y2=4xy+10y2;
(4)原式=(x2-y2)-(4x3y÷2xy)-(-8xy3÷2xy)=x2-y2-2x2+4y2=-x2+3y2.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,OB平分∠AOD,∠AOC=45°,∠COD=25°,则∠BOC=( )
如图,OB平分∠AOD,∠AOC=45°,∠COD=25°,则∠BOC=( )| A、5° | B、10° |
| C、15° | D、20° |
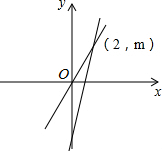 如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点.
如图,已知一次函数y=kx+b经过(-1,-5)且与正比例函数y=2x的图象相交于(2,m)点.
 如图,O为直线AB上一点,∠AOC=
如图,O为直线AB上一点,∠AOC= 在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.
在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图. 如图,∠ACD=110°,再需要添加一个条件:
如图,∠ACD=110°,再需要添加一个条件: