题目内容
2. 如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
如图,在Rt△ABC中,∠C=90°,AC=6,AB=10,DE垂直平分AB,分别交AB、BC于点D、E.求CE的长.
分析 由在Rt△ABC中,∠C=90°,AC=6,AB=10,根据勾股定理可求得BC的长,又由DE垂直平分AB,可得AE=BE,然后设CE=x,则AE=BE=8-x;利用勾股定理即可求得方程x2+62=(8-x)2,解此方程即可求得答案.
解答 解:在Rt△ABC中,∠C=90°,
∴$BC=\sqrt{A{B^2}-A{C^2}}=\sqrt{{{10}^2}-{6^2}}=8$;
∵DE垂直平分AB,分别交AB、BC于点D、E,
∴AE=BE;
设CE=x,则AE=BE=8-x;
在Rt△ACE中,∠C=90°,
∴CE2+AC2=AE2;
即x2+62=(8-x)2,
解得$x=\frac{7}{4}$,
即$CE=\frac{7}{4}$.
点评 此题考查了线段垂直平分线的性质以及勾股定理.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
相关题目
12.下列各组数中,不能构成直角三角形的是( )
| A. | 2,3,4 | B. | 5,12,13 | C. | 6,8,10 | D. | 3,4,5 |
4.下面所给的图形中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
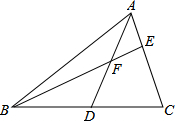 如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.
如图,在△ABC中,AD为BC边上的中线,E为AC上的一点,BE交AD于点F,已知AE=EF.求证:AC=BF.