题目内容
 如图,长方体的长、宽、高分别为3、4、5,则图中在表面上A到B的最短距离为
如图,长方体的长、宽、高分别为3、4、5,则图中在表面上A到B的最短距离为| 74 |
| 74 |
分析:分为三种情况展开,根据勾股定理求出线段AB的长度,再进行比较即可.
解答:解: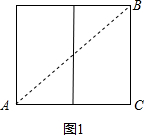
分为三种情况:
①如图1,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3+4=7,BC=5,
在Rt△ACB中,由勾股定理得:AB=
=
;
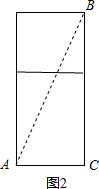
②如图2,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3,BC=5+4=9,
在Rt△ACB中,由勾股定理得:AB=
=
=3
;
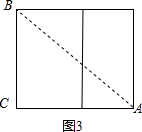
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3+4=7,BC=5,
在Rt△ACB中,由勾股定理得:AB=
=
;
即图①和图③求出的AB相等,
即在表面上A到B的最短距离是
,
故答案为:
.



分为三种情况:
①如图1,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3+4=7,BC=5,
在Rt△ACB中,由勾股定理得:AB=
| 72+52 |
| 74 |
②如图2,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3,BC=5+4=9,
在Rt△ACB中,由勾股定理得:AB=
| 32+92 |
| 90 |
| 10 |
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
∠ACB=90°,AC=3+4=7,BC=5,
在Rt△ACB中,由勾股定理得:AB=
| 72+52 |
| 74 |
即图①和图③求出的AB相等,
即在表面上A到B的最短距离是
| 74 |
故答案为:
| 74 |
点评:本题考查了平面展开-最短路线问题和勾股定理等知识点,关键是能画出展开图形并能求出符合条件的最短路线.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,长方体的长、宽、高分别为6cm,8cm,4cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是( )
如图,长方体的长、宽、高分别为6cm,8cm,4cm.一只蚂蚁沿着长方体的表面从点A爬到点B.则蚂蚁爬行的最短路径的长是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,求蚂蚁爬行的最短路程.
如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,求蚂蚁爬行的最短路程.
 如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长为( )cm.
如图,长方体的长、宽、高分别是8cm,4cm,4cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长为( )cm. 如图:长方体的长、宽、高分别是12,8,30,在AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去吃,有无数种走法,则最短路程是( )
如图:长方体的长、宽、高分别是12,8,30,在AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去吃,有无数种走法,则最短路程是( )