题目内容
14.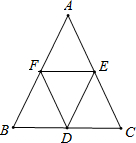 如图,点D、E、F分别是△ABC三边的中点,且AB=AC,则图中的四边形AEDF是菱形.
如图,点D、E、F分别是△ABC三边的中点,且AB=AC,则图中的四边形AEDF是菱形.
分析 四边形AEDF是菱形,利用三角形中位线的性质得出DE$\stackrel{∥}{=}$$\frac{1}{2}$AC,EF$\stackrel{∥}{=}$$\frac{1}{2}$AB,进而得出四边形AEDF为平行四边形,再利用AB=BC,可得DE=DF,即可得出四边形AEDF是菱形.
解答 解:四边形ADEF是菱形,
理由如下:∵D、E、F分别是△ABC三边的中点,
∴DE$\stackrel{∥}{=}$AC,EF$\stackrel{∥}{=}$$\frac{1}{2}$AB,
∴四边形AEDF为平行四边形.
又∵AC=AB,
∴DE=DF.
∴四边形AEDF为菱形.
点评 此题主要考查了三角形中位线的性质以及平行四边形的判定和菱形的判定等知识,熟练掌握菱形判定定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 等边三角形 |
5.已知a、b都是实数,且b$>\sqrt{a-2}-4\sqrt{2-a}+1$,化简$\frac{2}{b-1}$•$\sqrt{1-2b+{b}^{2}}$+1的结果是( )
| A. | 2 | B. | -2 | C. | 1 | D. | 3 |
9.在-2,0,2,$\sqrt{3}$这四个数中,最大的数是( )
| A. | -2 | B. | 2 | C. | $\sqrt{3}$ | D. | 0 |
19.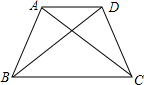 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )| A. | $4\sqrt{2}$ | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
3.某篮球队12名队员的年龄如表:
则这12名队员年龄的众数和中位数分别是18、19.
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
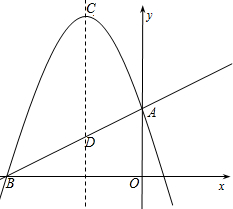 如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为直线x=-3.
如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为直线x=-3.