题目内容
5.已知a、b都是实数,且b$>\sqrt{a-2}-4\sqrt{2-a}+1$,化简$\frac{2}{b-1}$•$\sqrt{1-2b+{b}^{2}}$+1的结果是( )| A. | 2 | B. | -2 | C. | 1 | D. | 3 |
分析 先根据二次根式有意义的条件求出a的值,进而得出b的取值范围,再由二次根式的性质把原式进行化简即可.
解答 解:∵$\sqrt{a-2}$与$\sqrt{2-a}$有意义,
∴$\left\{\begin{array}{l}a-2≥0\\ 2-a≥0\end{array}\right.$,
∴a=2,
∴b>1,
∴1-b<0,
∴原式=$\frac{2}{b-1}$•$\sqrt{(1-b)^{2}}$+1
=$\frac{2}{b-1}$•(b-1)+1
=2+1
=3.
故选D.
点评 本题考查的是二次根式的性质与化简,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
16.下面的每组图形中,平移左图可以得到右图的是( )
| A. |  | B. |  | C. |  | D. |  |
13. 如图所示是一块长,宽,高分别是6cm,5cm和3cm的长方体木块,一只蚂蚁要从长方体木块的顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长度为10cm.
如图所示是一块长,宽,高分别是6cm,5cm和3cm的长方体木块,一只蚂蚁要从长方体木块的顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长度为10cm.
 如图所示是一块长,宽,高分别是6cm,5cm和3cm的长方体木块,一只蚂蚁要从长方体木块的顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长度为10cm.
如图所示是一块长,宽,高分别是6cm,5cm和3cm的长方体木块,一只蚂蚁要从长方体木块的顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长度为10cm.
17.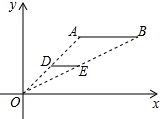 如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )
如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )
 如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )
如图,线段AB的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心,将线段AB缩小后得到线段DE,若DE=1,则端点E的坐标为( )| A. | (1,1) | B. | (1,2) | C. | (2,1) | D. | (2,2) |
 如图,已知在△ABC,A(-1,3),B(-3,-1).
如图,已知在△ABC,A(-1,3),B(-3,-1).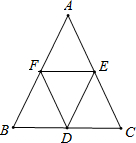 如图,点D、E、F分别是△ABC三边的中点,且AB=AC,则图中的四边形AEDF是菱形.
如图,点D、E、F分别是△ABC三边的中点,且AB=AC,则图中的四边形AEDF是菱形. 如图,DE是△ABC的中位线,若BC的长是10cm,则DE的长是5cm.
如图,DE是△ABC的中位线,若BC的长是10cm,则DE的长是5cm.