题目内容
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
(1)求证:△ACD∽△BAC;
(2)求DC的长.
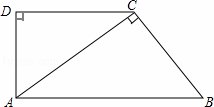
考点: 相似三角形的判定与性质;直角梯形.
分析: (1)由CD∥AB,得∠DCA=∠CAB,加上一组直角,即可证得所求的三角形相似.
(2)在Rt△ABC中,由勾股定理可求得AC的长,根据(1)题所得相似三角形的比例线段,即可求出DC的长.
解答: 解:(1)∵CD∥AB,
∴∠BAC=∠DCA,
又∵AC⊥BC,
∴∠ACB=90°,
∴∠D=∠ACB=90°,
∴△ACD∽△BAC;
(2)Rt△ABC中,AC=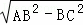 =8cm,
=8cm,
∵△ACD∽△BAC,
∴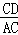 =
=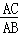 ,
,
即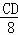 =
= ,
,
解得:DC=6.4cm.
点评: 此题考查了梯形的性质、相似三角形的判定和性质、勾股定理、熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的坐标为 .
的坐标为 . 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .

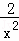 ﹣2=0
﹣2=0