题目内容
△ABC的内切圆半径为2cm，△ABC的周长为5cm，则△ABC的面积是 cm2．
5
考点： 三角形的内切圆与内心．
分析： 连OA，OB，OC．把三角形ABC分成三个三角形，根据内心的性质和三角形面积公式用三个三角形的面积的和表示三角形ABC面积，计算即可．
解答： 解：如图，⊙O是△ABC的内切圆，切点分别为D，E，F．
连OA，OB，OC，OD，OE，OF．
则OD⊥AB，OE⊥BC，OF⊥AC，且OE=OF=OD=2，
S△ABC=S△AOB+S△OBC+S△OAC
=
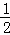×2×AB+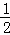×2×BC+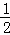×2×AC
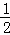=（AB+AC+BC）×2=5，
故答案为：5．
点评： 本题考查的是三角形的内心的性质，掌握三角形的内心是三角形三条角平分线的交点是解题的关键．
练习册系列答案
相关题目
+
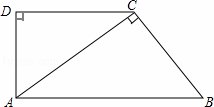
的值是（ ）
D． 1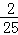
S△BCD？若存在，求出此时t的值；若不存在，说明理由；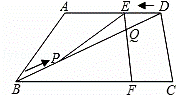
交于A（x1，y1），B（x2，y2）两点，则2x1y2﹣7x2y1= ．
