题目内容
6.已知a2+3a-1=0,求:(1)a-$\frac{1}{a}$;
(2)a2+$\frac{1}{{a}^{2}}$;
(3)a3-$\frac{1}{{a}^{3}}$.
分析 (1)已知等式两边除以a,变形即可求出所求式子的值;
(2)把(1)的结果两边平方,利用完全平方公式化简即可得到结果;
(3)原式利用立方差公式变形,将各自的值代入计算即可求出值.
解答 解:(1)∵a2+3a-1=0,
∴a-$\frac{1}{a}$=-3;
(2)把a-$\frac{1}{a}$=-3两边平方得:(a-$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$-2=9,
则a2+$\frac{1}{{a}^{2}}$=11;
(3)∵a-$\frac{1}{a}$=-3,a2+$\frac{1}{{a}^{2}}$=11,
∴原式=(a-$\frac{1}{a}$)(a2+$\frac{1}{{a}^{2}}$+1)=-36.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
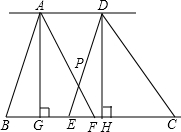 如图,AD∥BC,E,F是BC上的两点,AF,DE相交于点P,四边形EPAB的面积与四边形PFCD的面积相等,则BE=CF,请说明理由.
如图,AD∥BC,E,F是BC上的两点,AF,DE相交于点P,四边形EPAB的面积与四边形PFCD的面积相等,则BE=CF,请说明理由.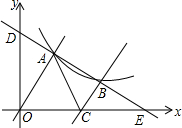 已知直线y=-$\frac{2}{3}$x+6与双曲线y=$\frac{k}{x}$(x>0)交于点A、B,把直线OA向右平移恰好经过点B,并与x轴交于点C,且OA:BC=2:1
已知直线y=-$\frac{2}{3}$x+6与双曲线y=$\frac{k}{x}$(x>0)交于点A、B,把直线OA向右平移恰好经过点B,并与x轴交于点C,且OA:BC=2:1 已知,如图,C为线段AB上除端点外的任意一点,AD∥BE,且∠D=∠1,∠E=∠2.求∠DCE的度数.
已知,如图,C为线段AB上除端点外的任意一点,AD∥BE,且∠D=∠1,∠E=∠2.求∠DCE的度数.