题目内容
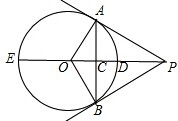 如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C.
如图,PA、PB是⊙O的两条切线,点A、B为切点,直线OP交⊙O于点D、E,交AB于点C.(1)写出圆中所有的垂直关系;
(2)写出图中所有的全等三角形;
(3)如果PA=4,PO=2,求半径OA的长.
考点:切线的性质,全等三角形的判定
专题:计算题
分析:(1)利用切线的性质得到OA⊥PA,OB⊥PB;再由切线定理得PA=PB,OP平分∠APB,然后根据等腰三角形的性质可判断AB⊥OP;
(2)根据“HL”判断△APO≌△BPO,△AOC≌△BOC;△APC≌△BPC;
(3)设⊙O的半径为r,则OP=OD+PD=r+2,利用勾股定理得到r2+42=(r+2)2,然后解方程即可.
(2)根据“HL”判断△APO≌△BPO,△AOC≌△BOC;△APC≌△BPC;
(3)设⊙O的半径为r,则OP=OD+PD=r+2,利用勾股定理得到r2+42=(r+2)2,然后解方程即可.
解答:解:(1)OA⊥PA,OB⊥PB,AB⊥OP;
(2)△APO≌△BPO;△AOC≌△BOC;△APC≌△BPC;
(3)∵PA⊙O的切线,
∴OA⊥PA,
在Rt△OAP中,设⊙O的半径为r,则OP=OD+PD=r+2,
∵OA2+PA2=OP2,
∴r2+42=(r+2)2,解得r=3,
即半径OA的长为3.
(2)△APO≌△BPO;△AOC≌△BOC;△APC≌△BPC;
(3)∵PA⊙O的切线,
∴OA⊥PA,
在Rt△OAP中,设⊙O的半径为r,则OP=OD+PD=r+2,
∵OA2+PA2=OP2,
∴r2+42=(r+2)2,解得r=3,
即半径OA的长为3.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.注意构造直角三角形,利用勾股定理计算线段的长.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
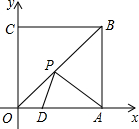 如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )
如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )| A、AC | B、BD | C、CD | D、不确定 |
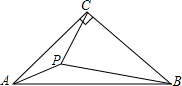 如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )
如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=1,PB=3,PC=2,则∠APC等于( )| A、105° | B、120° |
| C、135° | D、150° |
 如图所示,四边形ABCD中,DC∥AB,BC=2,AB=AC=AD=
如图所示,四边形ABCD中,DC∥AB,BC=2,AB=AC=AD=| 5 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
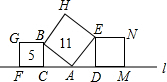 如图,直线l上方有三个正方形,若两个面积分别为5和11,则正方形DMNE的面积等于
如图,直线l上方有三个正方形,若两个面积分别为5和11,则正方形DMNE的面积等于