题目内容
6．
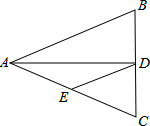如图，△ABC中，AB=AC=12，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长是（ ）| A． | 20 | B． | 12 | C． | 16 | D． | 13 |
分析 根据等腰三角形三线合一求出CD的长，根据直角三角形斜边上的中线等于斜边的一半求出DE的长，根据三角形的周长公式计算得到答案．
解答 解：∵AB=AC，AD平分∠BAC，
∴AD⊥BC，CD=$\frac{1}{2}$BC=4，
∵AD⊥BC，点E为AC的中点，
∴DE=EC=$\frac{1}{2}$AC=6，
∴△CDE的周长=CD+DE+EC=16，
故选：C．
点评 本题考查的是直角三角形的性质和等腰三角形的性质，掌握等腰三角形三线合一性质和直角三角形斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
相关题目
如图，已知AB∥CD，EF与AB，CD相交于点M，N，∠AMR=∠CNP，请你猜想MR与NP的位置关系？并说明理由．
如图是一个星形角度的求和问题，试利用你所学的多边形内角和定理计算图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和．
已知抛物线y=ax2+bx+c的部分图象如图所示，求此函数的解析式．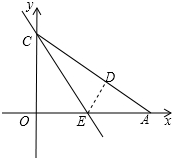
如图，在平面直角坐标系xOy中，直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴、y轴分别相交于点A、C，将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．
如图所示，已知AB∥CD，BC∥DE，试证明∠B=∠D．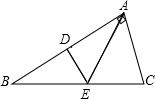
在Rt△ABC，∠BAC=90°，AB=8，AC=6，DE是AB边的垂直平分线，垂足为D，交边BC于点E，连结AE，则△ACE的周长是（ ）